不等式恒成立求参数取值范围问题，是高考的热点，同时也是高考难点，其通法是采用分类讨论，但过程往往十分繁琐，计算量十分庞大。当然也可以优先采用分离参数法，然而并非所有的问题都能奏效，尤其是遇到一些试题，其参数根本无法分离。

这时候，倘若能适当考虑区间端点的性质，先找到一个不等式成立的必要条件，从而缩小范围，然后再证明必要条件也是充分条件，那么即可求得结论。这种必要条件探路，再证充分性的方法，不妨称之为端点效应。

一·端点效应

1·必要条件缩小范围：

2·充分性求出结果：

二·高考题型归纳

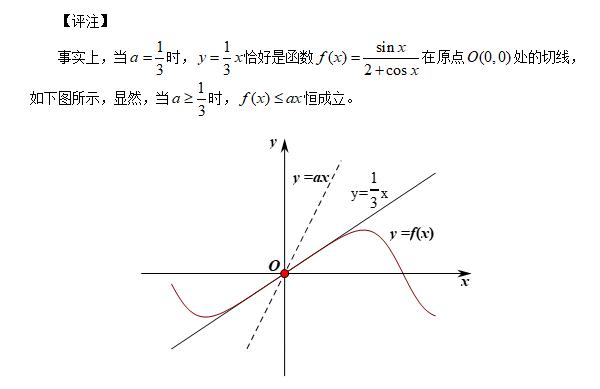
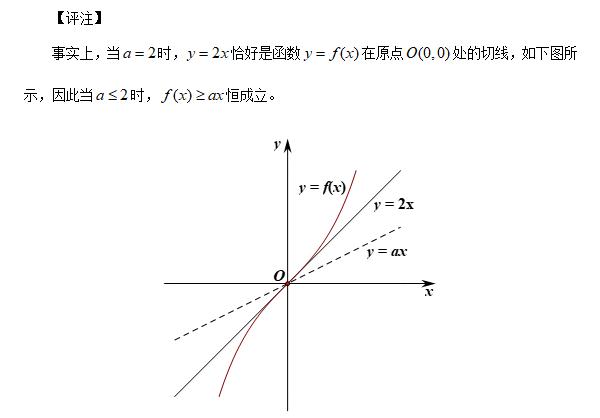
1·区间端点的函数值为零型：

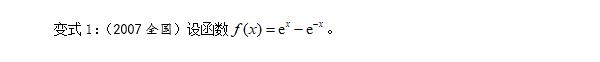
2·区间端点的函数值与导数值均为零型：