函数与方程思想之“换元法”在高中数学解题中的应用

一、换元法

在问题解决中，引入一个或几个新“元”代换问题中的旧“元”，使关于新元的问题能够解决；解决以后再将结果反演回去，得出旧元问题的结果，这种方法叫做换元法，也叫代换法。

“元”可以是任何意义下的基本元素，如未知数、变量、常量、几何元素等，也可以是一个整体，如代数式、图形等。本节来介绍下在解题过程中常用到的三种换元法。

第一换元法（旧式换为新元）

模式： f [ ψ(x) ] = f ( u ) ，其代换为 ψ(x) = u .

例题1、已知

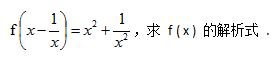
例题1图（1）

解：将已知等式改写为

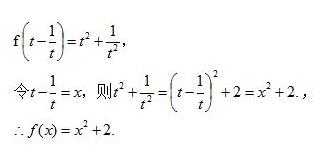
例题1图（2）

注：解题的关键是能把 t^2 + 1/t^2 凑成 t - 1/t 的表达式，所以这是凑法换元 。

例题2、求函数

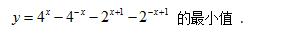
例题2图（1）

解：

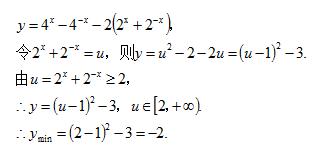
例题2图（2）

注：由函数 y = f ( x ）换元为 y = ψ（u），不但转换解析式也要注意转换定义域。

第二换元法（旧元换为新式）

模式： f（x）= f [ ψ（u）] ，其代换为 x = ψ(u) .

在方程的观点上，第二换元法是把方程 y = f ( x ) 化为参数方程 ： x = ψ(u) ，u = f（u）, （u为参数）。

例题3、解不等式

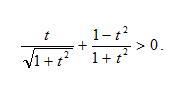
例题3图（1）

解：

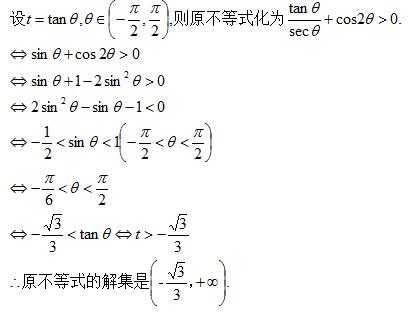
例题3图（2）

注：这是正切代换，遇见 √（1+t^2），可作代换 t = tanθ , θ∈（-π/2 ，π/2），其中 θ 的范围必须设出，保证代换是等价的。

例题4、求函数

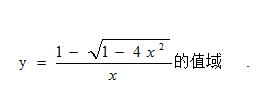
例题4图（1）

解：函数的定义域是 [-1/2 ，0 ）∪ （0 ， 1/2 ] ，

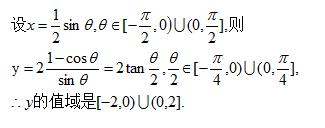
例题4图（2）

注：这是正弦代换，遇见 √（1-x^2），可作代换 x = sinθ , 或 x = cosθ，要根据 x 的范围确定 θ 的范围 。

第三换元法（旧式换为新式，及广义换元）

例题5、求函数

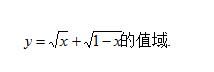
例题5图（1）

解：

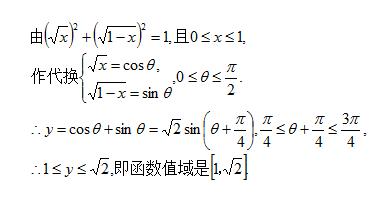
例题5图（2）

例题6、已知复数 z 满足 ∣2z + i∣ = 2 , 求 ∣3z - 4i∣ 的取值范围 。

解：（轨迹代换法）

设 W = 3z - 4i （W 是所求轨迹的动点），则 z = 1/3 （W + 4i）（z 是已知轨迹的动点）

代入已知轨迹方程 ∣2z + i∣ = 2 ，即 ∣2/3（W + 4i） + i∣ = 2 , 即 ∣W + 11/2 i∣ = 3 .

∴ 点 W 的轨迹是圆：圆心为 C （0，-11/2），半径为 r = 3 ，如下图所示

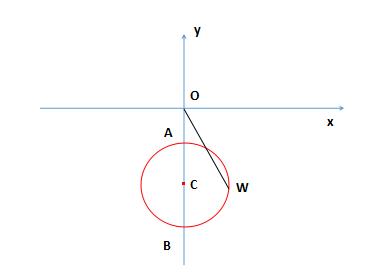
例题6图

∴ ∣OA∣ ≤ ∣W∣ ≤ ∣OB∣

其中 ∣OA∣ = 11/2 - 3 = 5/2 ， ∣OB∣ = 11/2 + 3 = 17/2 .

∴ 5/2 ≤ ∣3z - 4i∣ ≤ 17/2 .