一、匀速圆周运动
1.定义:物体的运动轨迹是圆的运动叫做圆周运动,物体运动的线速度大小不变的圆周运动即为匀速圆周运动。
2.特点:①轨迹是圆;②线速度、加速度均大小不变,方向不断改变,故属于加速度改变的变速曲线运动,匀速圆周运动的角速度恒定;③匀速圆周运动发生条件是质点受到大小不变、方向始终与速度方向垂直的合外力;④匀速圆周运动的运动状态周而复始地出现,匀速圆周运动具有周期性。
3.描述圆周运动的物理量:
(1)线速度v是描述质点沿圆周运动快慢的物理量,是矢量;其方向沿轨迹切线,国际单位制中单位符号是m/s,匀速圆周运动中,v的大小不变,方向却一直在变;
(2)角速度ω是描述质点绕圆心转动快慢的物理量,是矢量;国际单位符号是rad/s;
(3)周期T是质点沿圆周运动一周所用时间,在国际单位制中单位符号是s;
(4)频率f是质点在单位时间内完成一个完整圆周运动的次数,在国际单位制中单位符号是Hz;
(5)转速n是质点在单位时间内转过的圈数,单位符号为r/s,以及r/min.
4.各运动参量之间的转换关系:
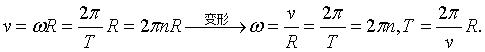

模型一:共轴传动
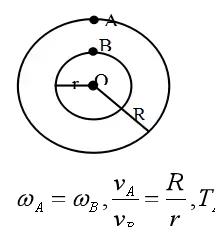
模型二:皮带传动
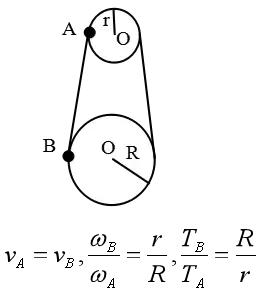
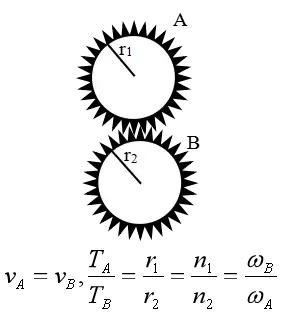
模型三:齿轮传动
练 习 题
1、一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )
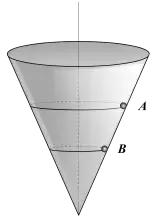
A.A球的角速度必小于B球的角速度
B.A球的线速度必小于B球的线速度
C.A球的运动周期必大于B球的运动周期
D.A球对筒壁的压力必大于B球对筒壁的压力
解析:小球A、B的运动状态即运动条件均相同,属于三种模型中的皮带传送。则可以知道,两个小球的线速度v相同,B错;因为RA>RB,则ωA<ωB,TA<TB,A.C正确;又因为两小球各方面条件均相同,所以,两小球对筒壁的压力相同,D错。所以A、C正确。
2、两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2 : 1,CD两点的半径之比也为2 : 1,则ABCD四点的角速度之比为 ,这四点的线速度之比为 。
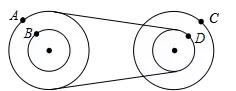
答案: 1:1:2:2 2∶1∶4∶2
二、向心加速度
1.定义:任何做匀速圆周运动的物体的加速度都指向圆心,这个加速度叫向心加速度。
注:并不是任何情况下,向心加速度的方向都是指向圆心。当物体做变速圆周运动时,向心加速度的一个分加速度指向圆心。
2.方向:在匀速圆周运动中,始终指向圆心,始终与线速度的方向垂直。向心加速度只改变线速度的方向而非大小。
3.意义:描述圆周运动速度方向方向改变快慢的物理量。
4.公式:
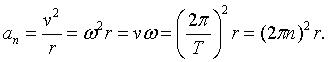
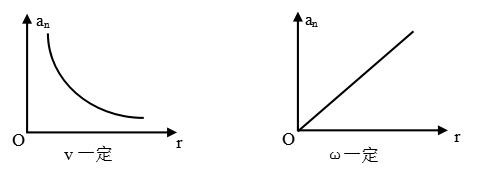
5.两个函数图像:
1、如图所示的吊臂上有一个可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩。在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起。A、B之间的距离以d = H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化。对于地面的人来说,则物体做( )
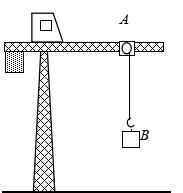
A.速度大小不变的曲线运动
B.速度大小增加的曲线运动
C.加速度大小方向均不变的曲线运动
D.加速度大小方向均变化的曲线运动
答案:AC
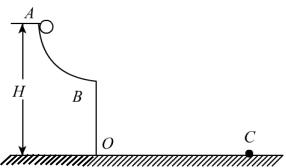
2、如图所示,位于竖直平面上的圆弧轨道光滑,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,到达B点时的速度为,最后落在地面上C点处,不计空气阻力,求:
(1)小球刚运动到B点时的加速度为多大,对轨道的压力多大;
(2)小球落地点C与B点水平距离为多少。
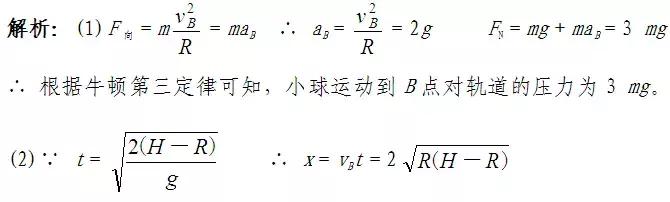
三、向心力
1.定义:做圆周运动的物体所受到的沿着半径指向圆心的合力,叫做向心力。
2.方向:总是指向圆心。
3.公式:
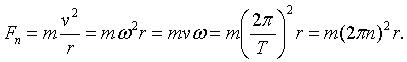
4.几个注意点:①向心力的方向总是指向圆心,它的方向时刻在变化,虽然它的大小不变,但是向心力也是变力。②在受力分析时,只分析性质力,而不分析效果力,因此在受力分析是,不要加上向心力。③描述做匀速圆周运动的物体时,不能说该物体受向心力,而是说该物体受到什么力,这几个力的合力充当或提供向心力。
四、变速圆周运动的处理方法
1.特点:线速度、向心力、向心加速度的大小和方向均变化。
2.动力学方程:合外力沿法线方向的分力提供向心力:
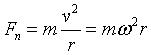
合外力沿切线方向的分力产生切线加速度:FT=mωaT。
3.离心运动:
(1)当物体实际受到的沿半径方向的合力满足F供=F需=mω2r时,物体做圆周运动;当F供<F需=mω2r时,物体做离心运动。
(2)离心运动并不是受“离心力”的作用产生的运动,而是惯性的表现,是F供<F需的结果;离心运动也不是沿半径方向向外远离圆心的运动。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论