速度排序题

1

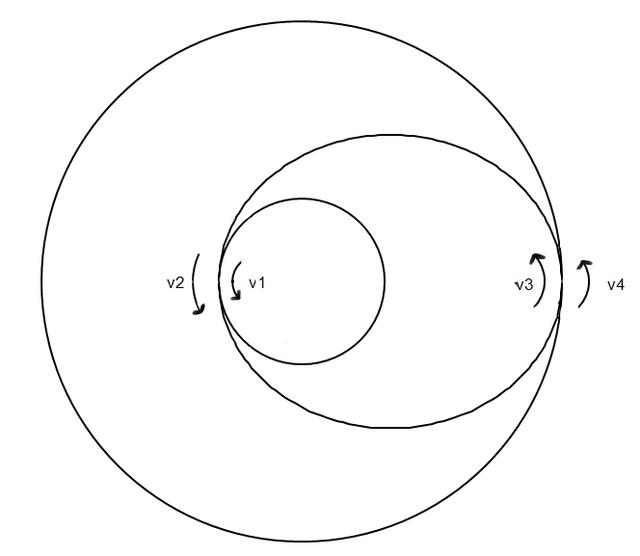
根据上图给予的轨道判断几个速度之间的大小关系。

碰到这种题目，不太会的同学就会死记大小关系，这样造成的后果就是对这类题目的本质把握不清，最终只能导致只能导出大小关系，却不能用之解题。

其实，这类题目的本质就是两条：

能量守恒

速度与距离的关系

首先，我们根据能量守恒，可以得出：由于从2到3的重力势能增加，所以v2>v3。（当然也可以通过开普勒三大定律中的第二定律，单位时间内扫过的面积相等导出）

然后，我们根据速度与距离的关系，可以导出剩余的关系。

还记得我们往期中提到的必记公式吗？

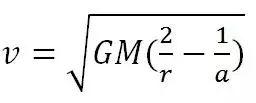
对于1和2，3和4，r相同而a不同，这样就可以导出v1<v2,v3<v4（当然，你也可以通过飞船起飞时老师强调的，起飞换轨加速来导出这两个大小关系）

对于1和4的圆形轨道，r=a，所以r增加，v减小，所以v1>v4.

最后，将这些大小关系整合可以得出v3<v4<v1<v2.

双星模型2

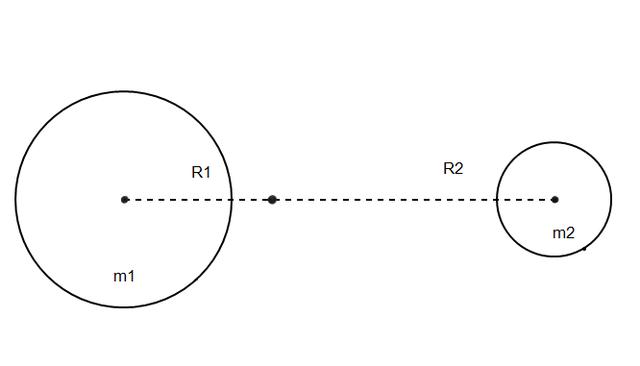
还记得我们往期说过的式子吗？

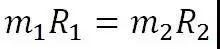
如果两边同时乘以一个角速度的平方，这个式子就可以理解为，两个星球所受向心力相等。

同时，我们列出两个万有引力与向心力的关系式

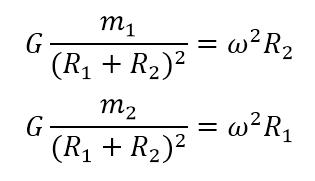
便可以得出

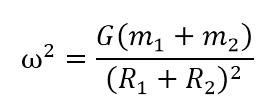
所以，角速度（或者说周期）只与总质量与两星之间的距离有关。

如果你下次遇到这样的题目，例如，A星球的质量跑到B星球上，那么两星饶转的周期是不会变的。

Tips：

遇到两星问题，中间最重要的就是列向心力与万有引力的关系式，通过等式变换，你就可以得到你想要的一切结论。

追及问题3

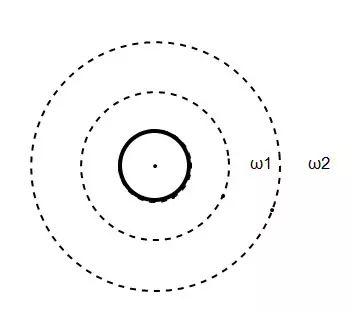
不知你是否在看到追及问题时茫然无措，其实，追及问题很简单，原则只有一个，那就是，化为角速度。

如果是速度，那么两者比较起来会十分麻烦；如果是周期，老师说的T1，T2的位置总是让人摸不着头脑。

不如将这些都转化为角速度，那么一个式子就可以搞定一切了。

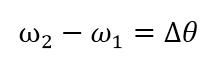
根据你的需要改变等式右边的值，那么题目就迎刃而解了。

细心观察这类问题，你会发现星球的追及问题其实就是我们做的直线追及问题在角速度上的体现，殊途同归，所有的问题其实都来源于我们之前所熟悉的事物。

F与R的关系4

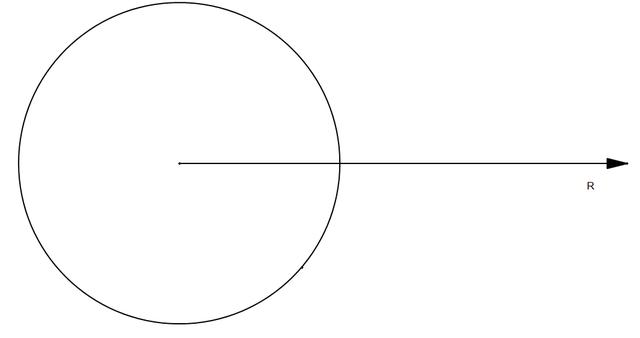
我们经常会遇到一个物体在星球的内部表面四处乱窜的问题，会要求我们计算做功，受力等等情况，而受力则是其中的基础。

首先，我们需要掌握一个书上没有但考试中经常出现的一个定律，球壳内部受力为零。（这点对于金属球内部的小球受到的电磁力也是成立的）

那么我们根据这一定理可以列出式子

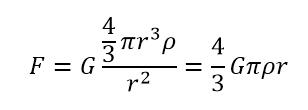
所以我们可以得出在星球内部时，物体受力与距离地心的距离成正比。

而当物体位于地球表面，受力就是mg啦。

当物体飞离地球表面在外太空进行圆形轨道的饶转时，我们可以根据受力等于万有引力得出受力与距离的平方成反比。

画成图像去记忆就是下面这张图啦。

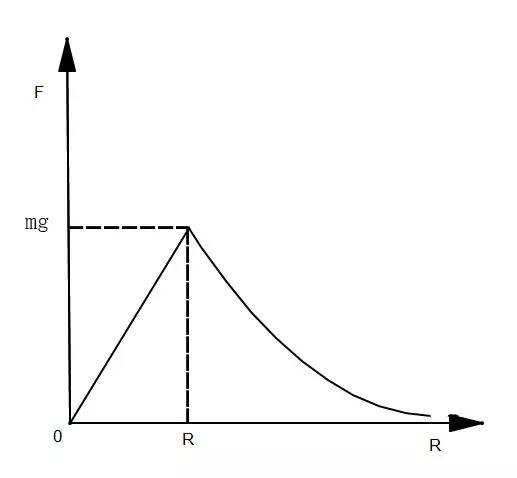
如果能够掌握这四个模型，大部分的万有引力题就不会出现问题了。