一·教材解读
新课标对导数与函数的单调性部分主要有三个要求:(1)了解函数单调性与导数的关系;(2)能利用导数研究函数的单调性;(3)会求不超过三次的多项式函数的单调区间。
课程标准对利用导数判断函数的单调性的要求可以分成两个层次:(1)要求掌握函数的单调性的定义以及了解导数与函数单调性的关系;(2)能利用导数求函数的单调区间,会画出函数的大致图象。
此部分类容属于导数的应用,是在学习了导数的概念、计算、几何意义等基础之上的内容。一方面,函数的单调性是高中数学中刻画函数变化最基本的性质;另一方面,导数是研究函数单调性、极值、最值等问题的重要工具。对于函数的单调性,高中数学分成了两个阶段,第一阶段是利用定义判断函数的单调性,第二阶段是利用导数研究函数的单调性。由于定义法判断函数单调性,局限性较大,因此需要利用导数法来弥补。
二·高考解读
高考中,对几何、不等式、函数的零点等问题的研究,往往都是建立在函数的单调性之上的,因此,利用导数来研究函数的单调性具有承上启下的作用。
函数的单调性在高考中往往以中档题出现,考查形式包括选择题、填空题和解答题的第一问,经常与参数结合,考查分类讨论的思想和分离参数法的应用。
三·高考中的单调性题型归纳
1·由单调性求参数的取值范围


2·由单调性求抽象函数不等式



3·利用导数判断单调性和求单调区间

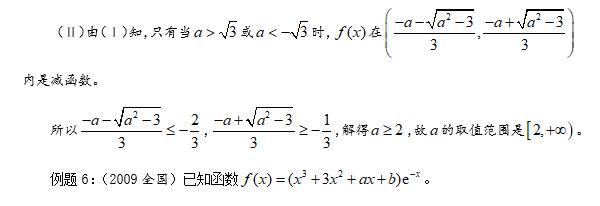

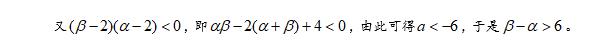

 加载中,请稍侯......
加载中,请稍侯......
精彩评论