梯形中辅助线的常见作法

一组对边平行，另一组对边不平行的四边形叫做梯形。

等腰梯形：有两条腰相等的梯形；直角梯形：有一个角是直角的梯形 。

一、从一底的两端，向另一底作垂线，构造矩形和三角形

例题1、如图，在梯形 ABCD 中 ，

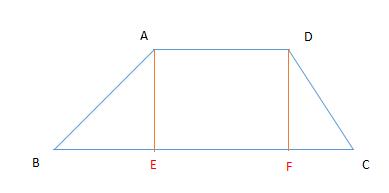
例题1图

过点 A、D 分别作 AE⊥BC、DF⊥BC ，垂足为点 E、F ，则 AE = DF = h(h为梯形ABCD的高) 。

求证：S梯形ABCD = 1/2 （AD+BC）· h

证明：

∵ S梯形ABCD = S△AEB + S矩形AEFD + S△DFC

S△AEB = 1/2 BE · h , S矩形AEFD = EF · h , S△DFC = 1/2 FC · h ;

∴ S梯形ABCD = 1/2 BE · h + EF · h + 1/2 FC · h

= 1/2 BE · h + 1/2 ( AD+ EF) · h + 1/2 FC · h

= 1/2 （AD+BC）· h

二、平移一腰，将梯形分为一个平行四边形和一个三角形

例题2、如图，在梯形 ABCD 中，AD∥BC ，AB = CD ，∠C = 60° ，AD = 15 ，BC = 49 ，求 CD 的长？

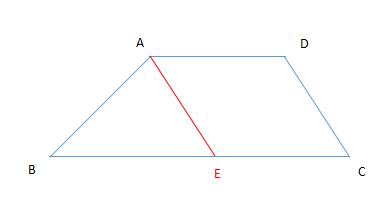
例题2图

解：过点 A 作 AE∥CD ，交 BC 于点 E ，则四边形 AECD 为平行四边形

∵ 四边形 AECD 为平行四边形

∴ AE = CD = AB ，∠AEB = ∠C = 60° , AD = EC

∴ △ABE 为等边三角形

∴ CD = BE = BC - EC = 49 - 15 = 34

三、延长梯形的两腰交于一点，构造三角形和梯形

例题3、如图，在梯形 ABCD 中，AD∥BC ，∠B = 50°，∠C = 80° ，AD = 5 , BC = 8 ,求 CD 的长？

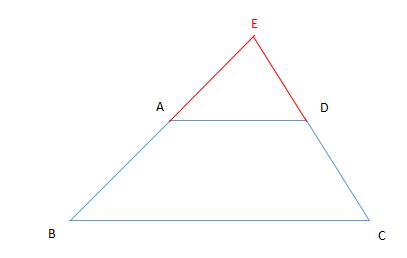
例题3图

解：延长 BA 和 CD 交于点 E ，在 △EBC 中

∵ ∠E + ∠B + ∠C = 180° （三角形内角和定理）

∴ ∠E = 180° - 50° - 80° = 50° = ∠B

∵ 在梯形 ABCD 中 ，AD∥BC

∴ ∠EAD = ∠B = ∠E

∴ △EAD 和 △EBC 都是等腰三角形

∴ ED = AD , EC = BC

∴ CD = EC - ED = BC - AD = 8 - 5 = 3

四、平移对角线，将梯形转化为三角形

例题4、如图，在梯形 ABCD 中，AD∥BC ，AC = 15 , BD = 20 , 高 DH = 12 ，求梯形 ABCD 的面积 ？

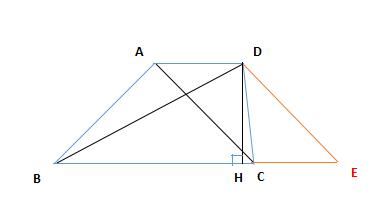
例题4图

解：过点 D 作 DE∥AC ，交 BC 延长线于点 E ，则四边形 ACED 为平行四边形

∵ S△BAD = S△CAD = S△DCE （等底同高，高是 DH）

∴ S梯形ABCD = S△DBE

在 Rt△BHD 中 ，由勾股定理得：

BH^2 = BD^2 - DH^2 = 20^2 - 12^2 = 16 ^2；

所以 BH = 16

在 Rt△DHE 中 ，由勾股定理得：

EH^2 = DE^2 - DH^2 = 15^2 - 12^2 = 81；

所以 EH = 9

∴ S梯形ABCD = S△DBE = 1/2 × DH × BE =1/2 × 12 × 25 = 150

五、连接一个顶点与另一腰中点并延长交另一底的延长线于一点

例题5、如图，在梯形 ABCD 中，AD∥BC ，点 H 为 CD 的中点，AB = AD + BC ；

求证：BH 平分∠ABC 。

例题5图

证明：

连接 AH 并延长交 BC 延长线于点 E

在 △AHD 和 △EHC 中

∵ AD∥BC ∴ ∠DAH = ∠E

∵ H 为 CD 的中点，∴ DH = CH

∵ ∠AHD = ∠EHC （对顶角相等）

∴ △AHD ≌ △EHC （AAS）

∴ AD = CE ，AH = EH

∵ AB = AD + BC ， BE = BC + CE

∴ AB = BE，即 △ABE 为等腰三角形

∴ BH 平分∠ABC （等腰三角形中三线合一）