八年级数学三角形的角、多边形及其内角专题训练

考点1、三角形内角和

例1、如图，在△ABC中，点D在AB上，点E在AC上，DE∥BC．若∠A=62°，∠AED=54°，则∠B的大小为（ ）

A、54° B、62° C、64° D、74°

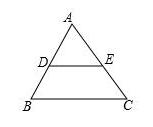
第1题图

例2、如图，在△ABC中，∠BAC=x°，∠B=2x°，∠C=3x°，则∠BAD=（ ）

A、145° B、150° C、155° D、160°

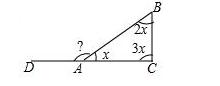
第2题图

例3、锐角三角形中任意两个锐角的和必大于（ ）

A、120° B、110° C、100° D、90°

例4、在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°-∠B，④∠A=∠B=∠C中，

能确定 △ABC 是直角三角形的条件有 (填序号) 。

例5、如图,在△ABC中,AB=AD=DC,∠BAD=26°,求 ∠B 和 ∠C 的度数。

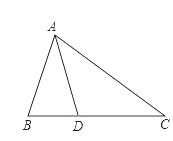
第5题图

例6、如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．

（1）求∠BAE的度数；

（2）求∠DAE的度数；

（3）探究：有同学认为，不论∠B，∠C的度数是多少，都有∠DAE= 1/2 （∠B-∠C）成立，你同意吗？

你能说出成立或不成立的理由吗？

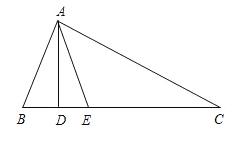
第6题图

举一反三：

1、若三角形三个内角的度数之比为1：2：3，则这个三角形是（ ）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

2、如图，点O是△ABC内一点，∠A=80°，∠1=15°，∠2=40°，则∠BOC等于（ ）

A、95° B、120° C、135° D、无法确定

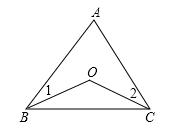
第2题图

3、如图，在△ABC中，∠ABC=50°，∠ACB=80°，BP平分∠ABC，CP平分∠ACB，则∠BPC的大小是（ ）

A、100° B、110° C、115° D、120°

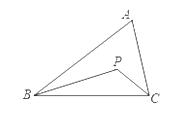
第3题图

4、如图，AD、BE、CF为 △ABC 的三条角平分线，则：∠1+∠2+∠3= 。

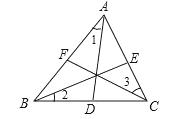
第4题图

5、生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获，如图两幅图都是由同一副三角板拼凑得到的：

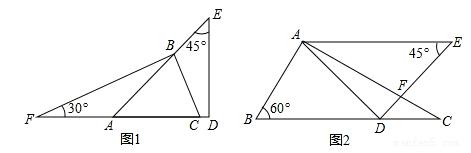
第5题图

（1）图1中的∠ABC的度数为 。

（2）图2中已知AE∥BC，则∠AFD的度数为 。

考点2、三角形外角

例1、如果三角形的一个外角小于与它相邻的内角，那么这个三角形一定是（ ）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形

例2、如图，在△ACB中，∠ACB=100°，∠A=20°，D是AB上一点．将△ABC沿CD折叠，使B点落在AC边上的B′处，

则∠ADB′等于（ ）

A、25° B、30° C、35° D、40°

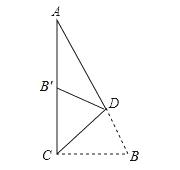
例题2图

例3、如图，D、E、F分别是△ABC三边延长线上的点，则∠D+∠E+∠F+∠1+∠2+∠3=____。

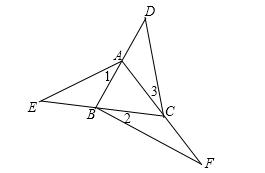
例题3图

例4、如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数。

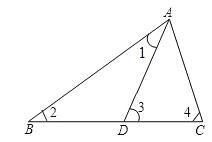
例题4图

例题5、如图，∠A＝90°，∠B＝21°，∠C＝32°，求∠BDC的度数。

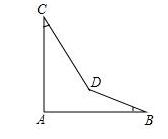
例题5图

举一反三：

1、直角三角形中两锐角平分线所交成的角的度数是（ ）

A、45° B、135° C、45°或135° D、都不对

2、小明把一副含45°，30°的直角三角板如图摆放，其中∠C=∠F=90°，∠A=45°，∠D=30°，则∠α+∠β等于（ ）

A、180° B、210° C、360° D、270°

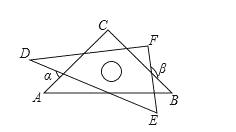
第2题图

3、如图，∠A=50°，∠ABO=28°，∠ACO=32°，则∠BDC=______度，∠BOC=______度。

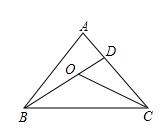
第3题图

4、如图，AE、OB、OC分别平分∠BAC、∠ABC、∠ACB，OD⊥BC，求证：∠1=∠2。

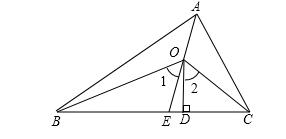
第4题图

5、如图，在△ABC中，点E在AC上，∠AEB=∠ABC。

（1）图1中，作∠BAC的角平分线AD，分别交CB、BE于D、F两点，求证：∠EFD=∠ADC；

（2）图2中，作△ABC的外角∠BAG的角平分线AD，分别交CB、BE的延长线于D、F两点，

试探究（1）中结论是否仍成立？为什么？

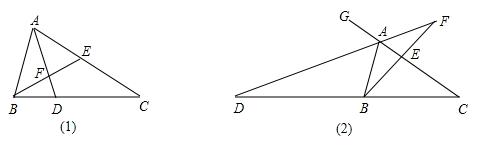
第5题图

考点3、多边形内角、外角

例1、一个多边形的内角是1440°，求这个多边形的边数是（ ）

A、7 B、8 C、9 D、10

例2、如图，∠1、∠2、∠3、∠4、∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=70°，则∠AED的度数是（ ）

A、110° B、108° C、105° D、100°

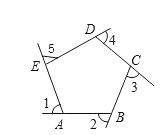
例题2图

例3、在水平的操场上，小明从A点出发，沿直线前进10米后，向左转30°，再沿直线前进10米，又向左转30°，…照这样走下去，他第一次回到出发点A时，一共走了________米。

例4、一个多边形的内角和是外角和的2倍，则这个多边形的边数是________。

例5、若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是（ ）

A、十三边形 B、十二边形 C、十一边形 D、十边形

例6、某同学在计算多边形的内角和时，得到的答案是1125°，老师指出他少加了一个内角的度数，你知道这个同学计算的是几边形的内角和吗？他少加的那个内角的度数是多少？

举一反三：

1、每个内角都相等的多边形，它的一个外角等于一个内角的 2/3 ，则这个多边形是（ ）

A、三角形 B、四边形 C、五边形 D、六边形

2、一个多边形的每一个外角都等于36°，则该多边形的内角和等于_______ °.

3、若一个多边形的内角和为900º，则这个多边形的边数是 。

4、如图，将一张四边形纸片沿直线剪开，如果剪开后的两个图形的内角和相等，下列四种剪法中，符合要求的是（ ）

第4题图

A、①② B、①③ C、 ②④ D、③④

5、如果一个凸多边形的所有内角从小到大排列起来，恰好依次增加的度数相同，设最小角为100°，最大角为140°，那么这个多边形的边数为多少？