一·圆锥曲线的技巧

重点掌握椭圆、双曲线、抛物线的定义，标准方程和简单几何性质，这些是圆锥曲线的基础，每年在高考试卷中都有体现。

掌握求曲线方程或轨迹方程的方法，曲线方程在高考中常常以解答题形式出现，难度一般较大。求曲线方程的方法有：（1）定义法；（2）直接法；（3）几何法；（4）相关点法；（5）参数法；（6）交轨法等。

加强直线与圆锥曲线的位置关系问题的训练，这是高考的热点也是难点。这类问题常常涉及圆锥曲线的性质，综合考查数学思想，考查逻辑推理能力和计算能力。其体型包括：（1）中点弦与对称问题；（2）弦长与面积问题；（3）定点与定值问题；（4）最值与范围问题；（5）证明与存在性问题等。

重视数学思想方法的归纳与提炼，达到优化思维，优化解题过程的目的。圆锥曲线中涉及的思想包括：（1）函数与方程的思想；（2）数形结合的思想；（3）分类讨论的思想；（4）转化与划归的思想；（5）设而不求的思想；（6）极限的思想等等。

二·圆锥曲线题型归纳

1·定点问题：

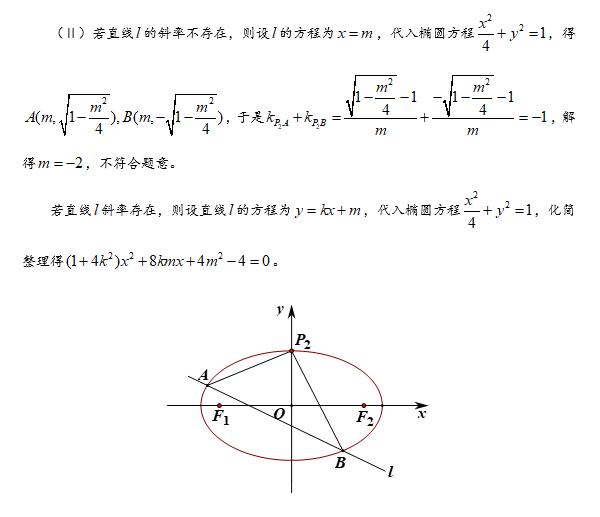
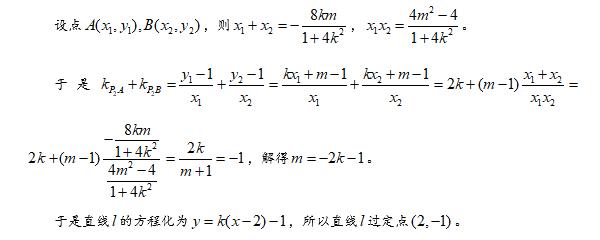
2·定值问题：

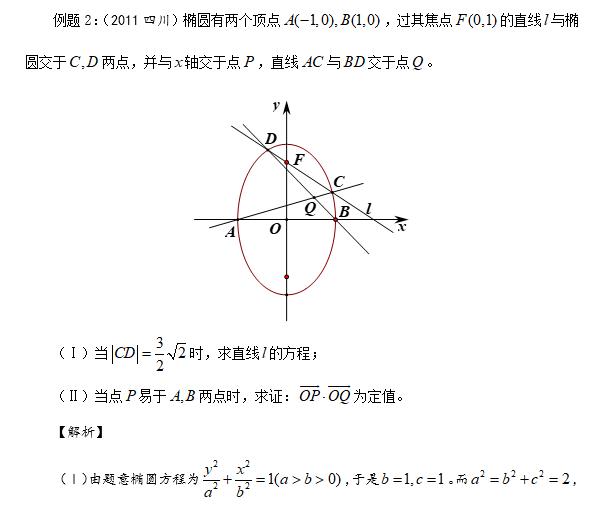
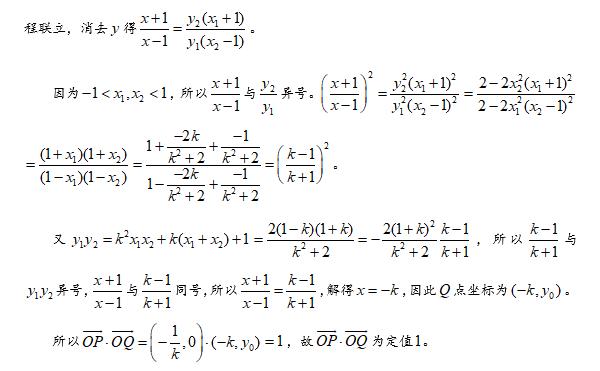
3·最值问题：

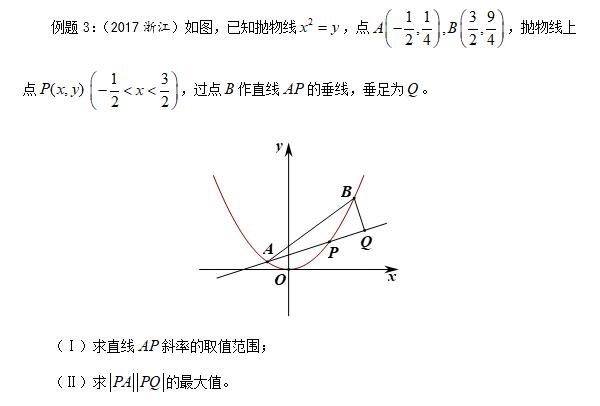
4·范围问题：

5·存在性问题：