(一)掌握一次函数的解析式的特征
一次函数解析式的结构特征:kx+b是关于x的一次二项式,其中常数b可以是任意实数,一次项系数k必须是非零数,即k≠0,而当b = 0,k≠0,y = kx既是正比例函数,是特殊的一次函数。
(二)应用一次函数解决实际问题
1、分清哪些是已知量,哪些是未知量,尤其要弄清哪两种量是相关联的量,且其中一种量因另一种量的变化而变化。
2、找出具有相关联的两种量的等量关系之后,明确哪种量是另一种量的函数。
3、在实际问题中,一般存在着三种量,如距离、时间、速度等等,在这三种量中,当且仅当其中一种量时间(或速度)不变时,距离与速度(或时间)才成正比例,也就是说,距离(s)是时间(t)或速度( )的正比例函数。
4、求一次函数与正比例函数的关系式,一般采取待定系数法。
(三)把握用待定系数法求函数解析式的一般步骤
1、依题意,设出含有待定系数的函数解析式。
2、把已知条件(自变量与函数对应值)代入解析式,得到关于待定系数的方程(组)。
3、解方程(组),求出待定系数。
4、将求得的待定系数的值代回所设的函数解析式,从而得到所求函数解析式。
(四)确定一次函数的表达式:
已知点A(x1,y1);B(x2,y2),请确定过点A、B的一次函数的表达式。
(1)设一次函数的表达式(也叫解析式)为y=kx+b。
(2)因为在一次函数上的任意一点P(x,y),都满足等式y=kx+b。所以可以列出2个方程:
y1=kx1+b①
y2=kx2+b②。
(3)解这个二元一次方程,得到k,b的值。
(4)最后得到一次函数的表达式。
(五)正确理解函数与方程及不等式之间的联系
1、直线y = kx+b与x轴交点的横坐标,是一元一次方程kx+b = 0的解,求直线y = kx+b与x轴的交点,可令y = 0,得到方程kx+b = 0,解方程得x =? ,?就是直线y = kx+b与x轴交点的横坐标,反之,由函数的图象也能求出对应的一元一次方程的解。
2、使一次函数y = kx+b的函数值y>0(或y<0> 的自变量的所有值,就是一元一次不等式kx+b>0(或kx+b<0)的解集。
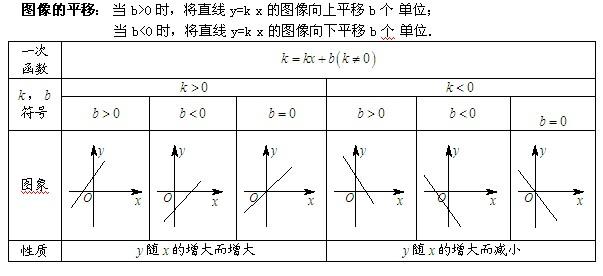
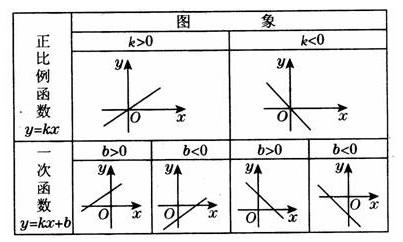
(六)一次函数的图象及性质:
1. 作法与图形:通过如下三个步骤:列表;描点;连线,可以作出一次函数的图象为一条直线。因此,作一次函数的图象只需知道两个点,并连成直线即可。
2. 性质:在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
3. k,b与函数图象所在象限。
当k>0时,直线必通过一、三象限,y随x的增大而增大;
当k<0时,直线必通过二、四象限,y随x的增大而减小。
当b>0时,直线必通过一、二象限;当b<0时,直线必通过三、四象限。
特别地,当b=O时,直线通过原点O(0,0)表示的是正比例函数的图象。
这时,当k>0时,直线只通过一、三象限;当k<0时,直线只通过二、四象限。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论