初二数学之反比例函数图象与图形面积问题

利用临界点求反比例函数图象与图形面积问题

例1.

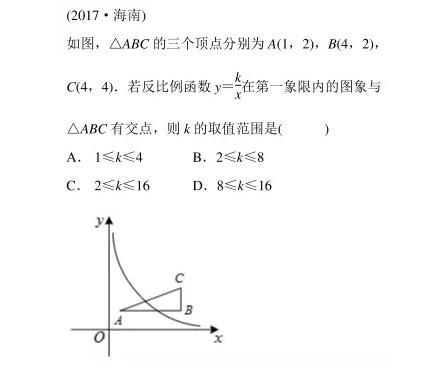
分析：

由于AB∥x轴，BC⊥x轴，易知△ABC是直角三角形，由于反比例函数在第一象限，k＞0，则当经过点A时，其横纵坐标的乘积最小，k值最小，经过点C时，其横纵坐标的乘积最大，k值最大．据此可得出k的取值范围．

解答：

过点A，则k＝2

过点C，则k＝16，2≤k≤16，选C

例2：

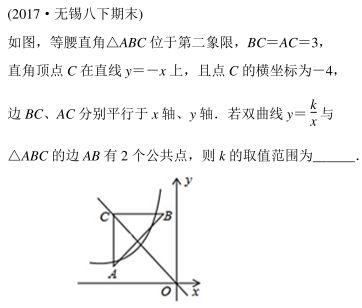
分析：

首先，我们可以根据点C的横坐标，求出点C的坐标，继而求出点A和点B的坐标，以及直线AB的解析式，易知AB⊥OC，设AB与OC交点为D，且D必为AB中点．

根据反比例函数的轴对称性，其中的一条对称轴是y＝－x，显然，当图象过点A时，也必然过点B，当图象过中点D时，与AB只有一个交点．

解答：

总结：

例1及例2，均是求反比例k的取值范围，那么只需关注临界点的情况．

如例1，考虑的是过点作坐标轴垂线段，两条垂线段与坐标轴围成面积的最大值和最小值，发现点A和点C是临界点．

而例2，则借助对称性，发现点A是临界点，AB的中点也是．因此，看到这样的题目，不要慌，找出关键临界点，计算下横纵坐标的积，k就解出来了！