五、十二个基本问题(后6个):
问题7、如图,在 Ll 上求点 A,在 L2 上求点 B,使 PA+AB 值最小 。
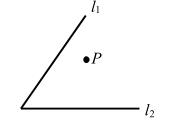
问题7图(1)
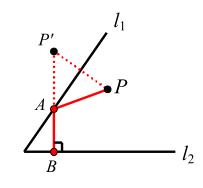
作法:如图,作点 P 关于L1 的对称点 P',作 P'B⊥L2 于点 B,交 L1 于点 A 。
问题7图(2)
原理:点到直线的距离,垂线段最短,PA+AB 的最小值为线段 P'B 的长 。
问题8、如图,点 A为L1 上一定点,点 B为 L2 上一定点,在 L2 上求点 M,在L1上 求 点 N , 使 AM+MN+NB 的值最小。
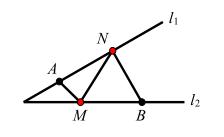
问题8图(1)
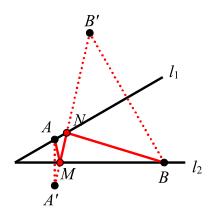
作法:如图,作点 A 关于L2 的对称点A',作点 B 关于L1 的对称点 B',连 A'B'交L2 于点 M,交L1 于点 N。
问题8图(2)
原理:两点之间线段最短,AM+MN+NB 的最小值为线段 A'B'的长。
问题9、如图,在直线 l 上求一点 P,使 ∣PB - PA∣ 的值 最小。
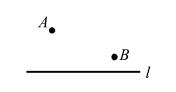
问题9图(1)
作法:如图,连 AB,作 AB 的中垂线与直线 l 的交点即为 P。
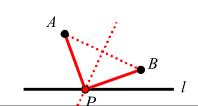
问题9图(2)
原理:垂直平分上的点到线段两端点的距离相等,故最小距离 ∣PB - PA∣ =0。
问题10、如图,在直线 l 上求一点 P,使 ∣PB- PA∣的值 最大 。
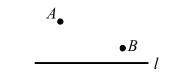
问题10图(1)
作法:如图,作直线 AB,与直线 l 的交点即为 P。
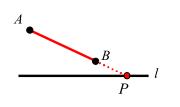
问题图(2)
原理:三角形任意两边之差小于第三边,∣ PB∣ - ∣ PA∣ ≤ ∣AB∣,故 ∣PB- PA∣ 的最大值 =AB。
问题11、如图,在直线 l 上求一点 P,使 ∣PA - PB∣ 的值 最大 。
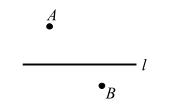
问题11图(1)
作法:如图,作 B 关于 l 的对称点 B'作直线 A B',与 l 交点即为 P。
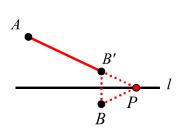
问题11图(2)
原理:三角形任意两边之差小于第三边, ∣PA - PB∣ ≤ AB', ∣PA - PB∣ 最大值 =AB'。
问题12、(费马点)如图,△ABC 中每一内角都小于120°,在△ABC 内求一点P,使 PA+PB+PC 值最小。
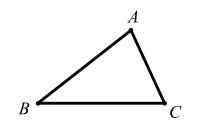
问题12图(1)
作法:如图,所求点为“费马点”,即满足∠APB=∠BPC=∠APC=120°,以 AB、AC为边向外作等边△ABD、△ACE,连 CD、BE 相交于 P,点 P 即为所求。
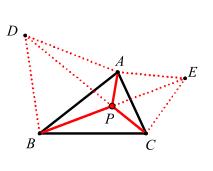
问题12图(2)
原理:两点之间线段最短,PA+PB+PC 最小值 =CD。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论