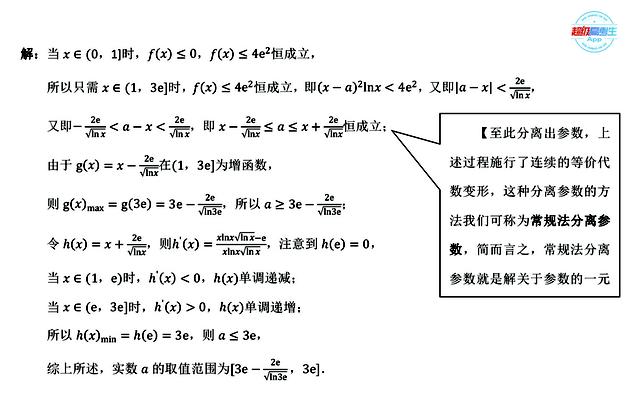
【评析】先缩小x的取值范围：x∈（1,3e]是关键，再用分离参数法完成就较为简单。应该说观察法在整个解题过程中比较重要的，首先要观察出有一部分范围，不等式是必然成立的，其次就是分离参数后的不等式左侧可以直接观察出函数是单调的，而右侧函数的极值点x=e，及其导函数的正负是通过观察其导函数表达式确定的．

通过上述解题过程，我认为中等生和优生可以不费丝毫力气地理解掌握。这个分离参数法的解法可以说遮住了压轴题的“风采”！

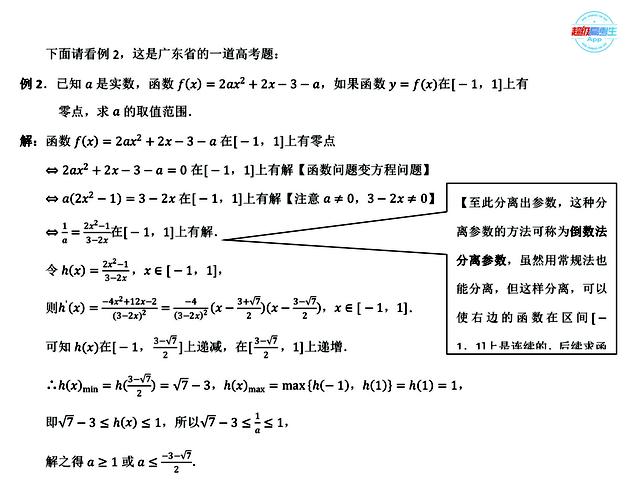
【评析】这道题虽含参数，但通过倒数法分离参数，规避了分类讨论的麻烦，是不是感觉简单多了。

上述通过换元的方式“孤立”参数或分离参数，我们可称为换元法分离参数。

这个题提供的参考答案，也是对参数进行分类讨论的，解题过程很长很繁琐，给学生按答案思路讲，恐怕收效甚微，于是我就想到换元法进行探索，结果很理想！

【评析】

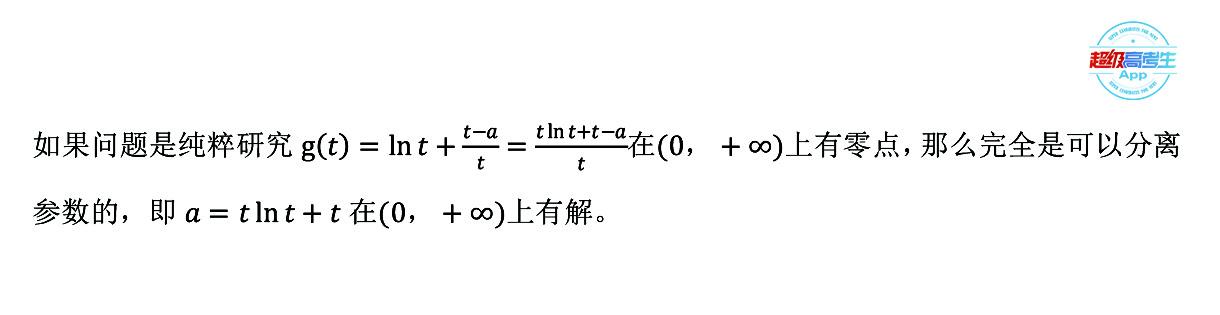
上述通过换元的方式“孤立”参数或分离参数，我们可称为换元法分离参数。这个题提供的参考答案，也是对参数进行分类讨论的，解题过程很长很繁琐，给学生按答案思路讲，恐怕收效甚微，于是我就想到换元法进行探索，结果很理想！

【评析】：第（1）问，由于使用了换元法，使参数a单独凸显出来，为简洁地解决问题做了很好的准备工作.第（2）问，进行分段讨论要有观察能力，后面能运用以直代曲，切线放缩的思想，进行放缩证明.

【阶段小结】通过以上四个实例，我们可以发现，常规法分离参数，倒数法分离参数，换元法分离参数，分类法分离参数，确实规避了对参数的分类讨论。这些方法其实是一种很自然的方法，学生一旦接触、领悟，定会豁然开朗，便会形成一种条件反射。当然，针对某些具体题型，分离参数法并不一定是最简单的方法，如一次函数、二次函数背景的命题，可能利用它们自身的函数性质解题会更简单。