在问题的解决中,把数量关系的精确刻画与空间形式的形象直观密切结合,调用代数与几何的双面工具,揭露问题的深层结构,达到解题的目的,这就是数形结合思想。
一、坐标法
通过选择适当的坐标系,建立数与形的对应关系,进行数与形的相互转化,从而实现问题解决的解题方法。
例如在解析几何中的公式和方程:
直线斜率、直线截距、两点间的距离、点到直线的距离、点到平面的距离、定比分点坐标、三点共线的充要条件、圆、椭圆、抛物线、双曲面、球等大都可以作为沟通数形间关系的桥梁,实现“数”向“形”的转化,达到“以形解数”的目的。
1、直线斜率模式
如果待解问题涉及形如 (a+b)/(c+d) 的式子,可转化为直线斜率 k = (y0 - y)/(x0 - x)的形式,根据斜率的几何解释和相关条件研究斜率的变化规律,实现问题解决。
例题1、如果数 x , y 满足等式 (x - 2)^2 + y^2 = 3 , 那么 y/x 的最大值是 ()
A、1/2 B、√2/3 C、√3/2 D、√3
解题思路:
待解问题 y/x = (0 - y)/(0 - x)具有直线斜率的形式,可把它看成过定点 (0,0)和动点(x,y)的直线斜率 k ,而 x,y 满足等式
(x - 2)^2 + y^2 = 3 , 其几何意义是动点(x,y)的轨迹是以(2,0)为圆心 ,√3 为半径的圆,借助图形可得 k 的最大值。
解:如图,建立平面直角坐标系,设动点 P(x,y),其中 x , y 满足等式 (x - 2)^2 + y^2 = 3 , 因而 P(x,y)是以点 A(2,0)为圆心,半径为 √3 圆上的动点。
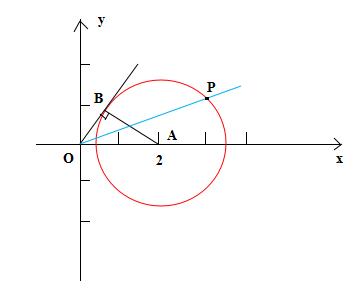
例题1图
过定点(0,0)和动点 P(x,y)的直线的斜率是 k = y/x 。从上图容易看出,当直线 OP 与 ⊙A 的上半圆相切时, k 取最大值。
设相应得切点为 B ,则 Kmax = ∣AB∣/∣OB∣ = √3 / 1 = √3 ,故选 D 。
2、直线截距模式
如果待解问题涉及形如 a • f(t)+ b • φ(t)的式子,可转化为直线 m = ax + by 的形式,可根据直线截距的几何意义和相关约束条件研究截距变化规律,实现问题解决。
例题2、求函数 S = x + √(1 - x^2 ) 的最大值和最小值。
解题思路:
函数 S = x + √(1 - x^2 ) 具有 S = a • f(t)+ b • φ(π)的形式,令 y = √(1 - x^2 ) ,即 x^2 + y^2 = 1 (y ≥ 0),它的几何意义是半圆,借助图形可得 S 的最大值和最小值。
解:建立平面直角坐标系 xOy ,令 y = √(1 - x^2 ) ,动点 P(x,y),其坐标 x , y 满足方程 S = x + y 和 y = √(1 - x^2 );
即 y = -x + S ① 和 x^2 + y^2 = 1(y ≥ 0)② ;
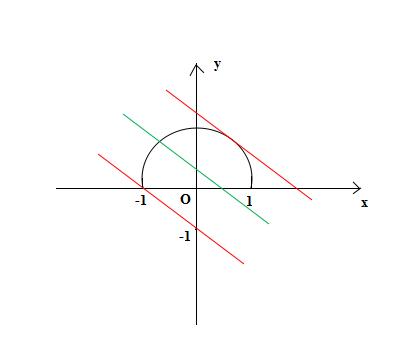
例题2图
① 的几何意义是表示过动点 P(x,y)的相互平行的直线系,它们在纵轴上的截距为 S ;
② 的几何意义是 P(x,y)以 (0,0)为圆心,1 为半径的上半圆上的动点。
由图可知,
当 ① 与半圆相切时,纵截距 S 取得最大值,其值可由原点到直线 y = -x + S 的距离是圆半径 1 的等式关系得到,
即 S/√2 = 1 , Smax = √2 ;
当 ① 过点 A(-1,0)点时 S 取得最小值 Smin = -1 。
3、两点间距离模式
如图待解问题涉及或经过恒等变形可转化为 √[(x-x1)^2 + (y-y1)^2] 的形式,可用
两点之间的距离 d = √[(x-x1)^2 + (y-y1)^2] 模式,在根据相关约束条件研究 d 的变化规律,实现问题解决。
例题3、求函数 y = √ [x^2 + 2x + 2] + √ [x^2 - 6x + 10] 的最小值 。
解题思路:
函数 y = √ [x^2 + 2x + 2] + √ [x^2 - 6x + 10] = √ [(x+1)^2 +1^2] + √ [(x-3)^2 +1^2]
具有两点间的距离模式,可把 √ [(x+1)^2 +1^2] 解释为动点 P(x,0)与定点 A(-1,-1)间的距离;
√ [(x-3)^2 +1^2] 是动点 P(x,0)与定点 B(3,1)间的距离,而点 P(x,0)在 x 轴上运动,借助图形容易得到函数的最小值。
解:建立如下图所示的直角坐标系,设 P(x,0),A(-1,-1),B(3,1)
则 y = √ [x^2 + 2x + 2] + √ [x^2 - 6x + 10] = ∣PA∣ + ∣PB ∣ ≥ ∣CA∣ + ∣CB ∣ =∣ AB∣ ;
因而 ymin = ∣ AB∣ = √[(3+1)^2 + (1+1)^2 ] = 2√5 。
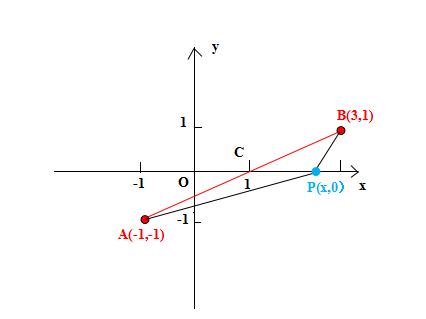
例题3图
 加载中,请稍侯......
加载中,请稍侯......
精彩评论