一、解题思路
1、利用图形想到三角形全等,相似及三角函数;
2、分析题目,了解有几个动点,动点的路程,速度(动点怎么动);
3、结合图形和题目,得出已知或能间接求出的数据;
4、分情况讨论,把每种可能情况列出来,不要漏;
5、动点一般在中考都是压轴题,步骤不重要,重要的是思路;
6、动点类题目一般都有好几问,前一问大都是后一问的提示,就像几何探究类题一样,如果后面的题难了,可以反过去看看前面问题的结论。
二、三角形全等之动点问题(题型讲解)
例题1、如图,AB=18 cm,动点 P 从点 A 出发,沿 AB 以2 cm/s 的速度向点 B 运动,动点 Q 从点 B 出发,沿 BA 以1 cm/s 的速度向点 A 运动。P,Q 两点同时出发,当点 P 到达点 B 时,点 P,Q 同时停止运动。设点 P 运动的时间为 t 秒,请回答下列问题:
(1)AP= 2t ,QB= t (含t的式子表达);
(2)在 P,Q 相遇之前,若 P,Q 两点相距 6 cm,则此时 t 的值为 4s 。

例题1图
知识点总结:
由点 速度已知 的运动产生的几何问题称为 动点 问题,这类问题的解决方法如下:
1、 研究 背景图形 ,标注;2、分析 运动过程 ,分段;3、表达 线段长度 ,建立等式 。
例题2、如图,在矩形 ABCD 中,AB = 4,AD = 10,点 E 为边 AD 上一点,且 AE = 7。动点 P 从点 B 出发,以每秒 2 个单位的速度沿 BC 向点 C 运动,连接 AP,DP。设点 P 运动时间为 t 秒。
(1)当 t = 1.5 时,△ABP 与 △CDE 是否全等?请说明理由;(2)当 t 为何值时,△DCP ≌ △CDE 。
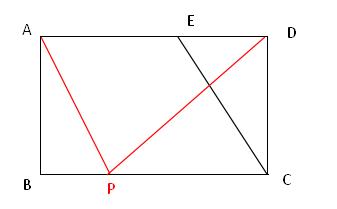
例题2图
解:(1)当 t = 1.5 时,△ABP ≌ △CDE;
理由如下:如图,由题意得 BP = 2t
∴当 t = 1.5 时,BP = 3
∵AE = 7,AD = 10 ∴ DE = 3 ∴ BP = DE
在矩形ABCD中 AB=CD,∠B =∠CDE
在 △ABP 和 △CDE 中
∵ AB=CD,∠B =∠CDE , BP = DE
∴ △ABP ≌ △CDE(SAS)
(2)如图,由题意得 BP = 2t
∵BC=10 ∴ CP =10 - 2t
若使△DCP≌△CDE,则需CP=DE
即10-2t = 3,t = 3.5
∴ 当 t = 3.5 时,△DCP ≌ △CDE 。
例题3、如图,在等腰 Rt△ABC中,∠ACB=90°,AC=CB,F 是 AB 边上的中点,点 D、E 分别在 AC、BC 边上运动,且始终保持AD=CE。连接 DE、DF、EF。
(1)求证:△ADF ≌ △CEF ;
(2)试证明 △DFE 是等腰直角三角形 。
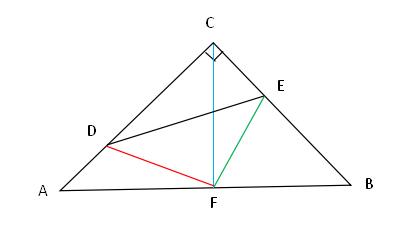
例题3图
证明:
(1)∵ 在 Rt△ABC 中,∠ACB=90°,AC=CB ,F 是 AB 边上的中点
∴ CF ⊥AB , CF 平分 ∠ACB (等腰三角形中角平分线、中线、高 三线合一)
∴ AF = CF , ∠A = ∠FCB = 45°
在 △ADF 和 △CEF 中
∵ AF = CF , ∠A = ∠FCB = 45° , AD = CE
∴ △ADF ≌ △CEF (SAS)
(2)由(1)知 △ADF ≌ △CEF 得 DF = EF ,∠AFD = ∠CFE
∵ ∠AFD + ∠DFC = ∠AFC = 90°
∴ ∠CFE + ∠DFC = ∠DFE = 90°
∴ △DFE是等腰直角三角形
例题4、如图,在梯形 ABCD 中,AD∥BC,∠ABC=90°,AD=12,BC=24,动点 P 从点 A 出发以每秒1个单位的速度沿 AD 向点 D运动,动点 Q 从点 C 出发以每秒 2 个单位的速度沿 CB 向点 B 运动,P,Q 同时出发,当点 P 停止运动时,点 Q 也随之停止,连接PQ,DQ 。设点 P 运动时间为 t 秒,试求当 t 为何值时,△PDQ ≌ △CQD 。
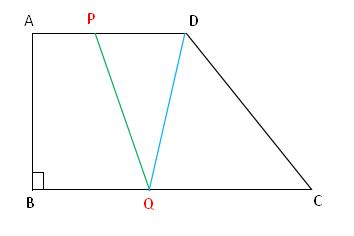
例题4图
解:如图,由题意得 AP = t,CQ = 2t
∵ AD = 12 ∴ DP = 12 - t
要使 △PDQ ≌ △CQD,则需 DP = QC
即12 - t = 2t ,t = 4
∴ 当 t = 4 时,△PDQ ≌ △CQD (SAS)
例题5、如图,在△ABC中,AB=AC=10 cm,BC=8 cm,点 D 为 AB 的中点,动点 P 在线段 BC上以每秒 3 cm 的速度由点 B 向点 C运动,同时动点 Q 在线段 CA 上由点 C 向点 A 运动。设点 P 运动时间为 t 秒,当 t 为何值时 △BPD ≌ △CQP ,试求此时 t 的值及动点 Q 的运动速度 。
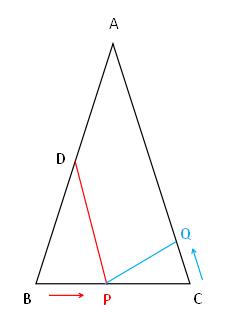
例题5图
解:如图,由题意得 BP = 3t
∵ BC = 8 ∴ PC = 8 - 3t
∵ AB =10,D 为 AB 中点
∴BD= 1/2 AB = 5
① 要使 △BDP ≌ △CPQ ,则需 BD = CP,BP = CQ
即 5 = 8 - 3t,t =1 ∴ CQ = 3t = 3
则 Q 的速度为 SQ = S / t = 3 / 1 = 3 (cm/s)
即当 t =1,Q 的速度为每秒 3 cm 时,△BDP ≌ △CPQ 。
② 要使 △BDP ≌ △CQP,则需 BP= CP,BD = CQ
即 3t = 8 - 3t,CQ = 5 ∴ t = 4/3
则 Q 的速度为 SQ = S / t = 5 × 3/4 = 15/4 (cm/s)
即当 t = 15/4 (cm/s),Q的速度为每秒 15/4 cm时,△BDP ≌ △CQP。
综上所述,当 t =1时,Q的速度为每秒3cm 或 t = 4/3 时 ,Q的速度为每秒 15/4 cm时,△BPD ≌ △CQP 。
例题6(单动点问题)、如图,在矩形 ABCD 中,AB=DC=4,AD=BC=5。延长BC到 E,使 CE = 2,连接DE。
动点 P从点 B 出发,以每秒2个单位的速度沿 BC-CD-DA 向终点 A 运动,设点 P 运动时间为 t 秒。
(1)请用含 t 的式子表达 △ABP 的面积 S;
(2)是否存在某个 t 值,使得△DCP和△DCE全等?若存在,请求出所有满足条件的t值;若不存在,请说明理由。
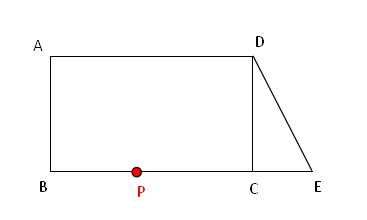
例题6图
解:(1)
① 当动点 P 在 BC上时,
如图,由题意得BP = 2t(0≤ t ≤ 2.5)
∴ S△ABP = 1/2 AB • BP = 1/2 × 4 × 2t = 4t ;
② 当动点 P 在CD上时,(2.5 < t ≤ 4.5)
∴ S△ABP = 1/2 AB • BC = 1/2 × 4 × 5 = 10 ;
③ 当动点 P 在 AD上时,由题意得AP=14-2t(4.5 < t ≤ 7)
∴ S△ABP = 1/2 AB • AP = 1/2 × 4 × (14-2t) = 28 - 4t 。
(2)
① 当动点 P 在 BC上时,
如图,由题意得BP=2t
要使△DCP≌△DCE,则需CP=CE
∵ CE=2 ∴ 5 - 2t = 2,t = 1.5
即当 t =1.5时,△DCP ≌ △DCE
② 当动点 P 在 CD 上时,不存在 t 使 △DCP 和 △DCE 全等
③ 当动点 P 在 AD 上时,由题意得 BC + CD + DP = 2t
∵ BC=5,CD=4,∴DP = 2t - 9
要使△DCP≌△CDE,则需DP=CE
即2t-9=2,t=5.5 即当 t =5.5 时,△DCP ≌ △CDE。
综上所述,当 t=1.5 或 t= 5.5 时,△DCP 和 △DCE全等。
例题7(双动点问题)、如图,在矩形 ABCD 中,AB=CD=3 cm,AD=BC=5 cm,动点 P 从点 B 出发,以每秒1 cm的速度沿 BC 方向向点 C 运动,动点 Q 从点 C 出发,以每秒2 cm的速度沿 CD-DA-AB 向点 B 运动,P,Q 同时出发,当点 P 停止运动时,点 Q 也随之停止,设点 P 运动时间为 t 秒。请回答下列问题:
(1)请用含 t 的式子表达△CPQ 的面积 S,并直接写出 t 的取值范围;
(2)是否存在某个t 值,使得△ABP和△CDQ全等?若存在,请求出所有满足条件的t值;若不存在,请说明理由。
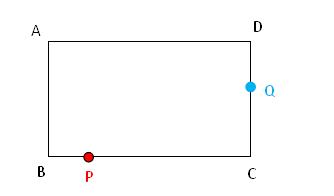
例题7图
解:(1)
① 当动点 Q 在 CD上时,
如图,由题意得 CQ =2t,BP = t
∴ CP = 5 - t(0 ≤ t ≤1.5)
∴ S△CPQ = 1/2 CP • CQ = 1/2 (5 - t)• 2t = 5t - t^2 ;
② 当动点 Q 在 DA上时,(1.5 < t ≤ 4)
∴ S△CPQ = 1/2 CP • CD = 1/2 (5 - t)× 3 = 7.5 - 1.5t ;
③ 当动点 Q 在AB上时,由题意得 BQ =11-2t(4 < t ≤ 5)
∴ S△CPQ = 1/2 CP • BQ = 1/2 (5 - t)× (11 - 2t) = t^2 - 21t / 2 + 55/2 。
(2)
① 当动点 Q 在 CD上时,不存在 t 使△ABP和△CDQ全等
② 当动点 Q 在 AD上时,
由题意得 DQ =2t-3 要使 △ABP ≌ △CDQ,则需 BP = DQ
∵ DQ = 2t-3,BP = t ∴ t = 2t - 3,t = 3
即当 t = 3 时,△ABP ≌ △CDQ 。
③ 当动点 Q 在 AB上时,不存在 t 使△ABP和△CDQ全等
综上所述,当 t = 3 时,△ABP 和 △CDQ 全等。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论