高考数学，典型例题分析8：数列求和相关综合题型

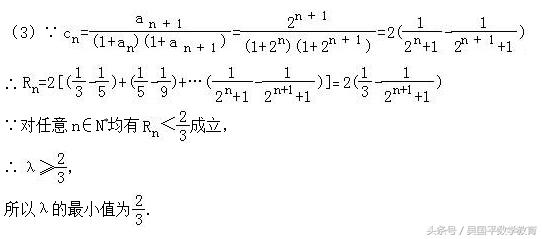
考点分析：

数列递推式；数列的求和．

题干分析：

（1）利用已知条件推出an+1=2an，数列{an}为等比数列，公比q=2，求出通项公式．

（2）推出bn=2n（5-n），方法一：通过T1＜T2＜T3＜T4=T5＞T6＞推出结果．方法二利用错位相减法求和，当1≤n＜4，Tn+1＞Tn，当n=4，T4=T5，当n＞4时，Tn+1＜Tn，

综上，当且仅当k=4或5时，均有Tk≥Tn．

（3）利用裂项求和，通过对任意n∈N*均有Rn＜2/3成立，求解即可．

解题反思：

数列求和是数列中的一个重要内容，是数列知识的综合体现，也是高考的热点。

数列是以正整数集或它的有限子集为定义域的函数，是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项(通常也叫做首项)，排在第二位的数称为这个数列的第2项排在第n位的数称为这个数列的第n项，通常用an表示。

数列求和是指对按照一定规律排列的数进行求和，即求Sn。

实质上是求{Sn}的通项公式，应注意对其含义的理解。

常见的求和方法有公式法、错位相减法、倒序相加法、分组法、裂项法、数学归纳法、通项化归等。