1. 正方体展开图全解

对于空间感不是太好的孩子来说，这类题目很容易弄混，但是这又是必考的内容。所以可以用下面这种口诀配合着图形进行记忆和学习。

其实总共只有11种展开图最终能拼成一个正方形，其中又分为4个大类。具体如下：

【口诀】：

中间四个面，上下各一面（共6种摆法-141）

中间三个面，一二隔河见（3种摆法-132/231）

中间二个面，楼梯天天见（1种摆法-222)

中间没有面，三三连一线（1种摆法-33）

“田”“凹”应弃之（出现田和凹这种形状的展开图，肯定无法拼成正方形）

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

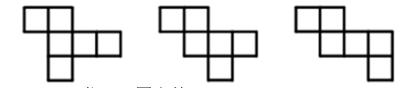
口诀：中间三个面，一二隔河见（二三位置是固定的）

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

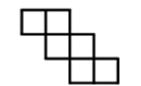
口诀：中间二个面，楼梯天天见

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

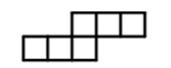
中间没有面，三三连一线（1种摆法-33）

2 . 已知两数的和与差，求这两个数。

孩子们在做这种类型题目时，经常会出现思维混乱的状况，不知道从何下手。

【口诀】：

和加上差，越加越大； 除以 2，便是大的；（即大数对于和加差后除2）

和减去差，越减越小； 除以 2，便是小的。（即小数等于和减差后除2）

例：已知两数和是20，差是 4，求这两个数。按口诀进行进行计算，大的数=（20+4）/2=12，小的数=（20-4）/2=8。

3. 鸡兔同笼问题

这道题是我国古算书《孙子算经》中著名的数学问题，也是必考题目之一。不过只要记住下面的口诀就很容易解答了。

【口诀】：

假设全是鸡，假设全是兔。

多了几只脚，少了几只足？

除以脚的差，便是鸡兔数。

例1：鸡免同笼，共有头 72 ，共有脚 240，求鸡兔数。

求兔时，假设全是鸡，则免子数=（240-72X2）/（4-2）=48

求鸡时，假设全是兔，则鸡数 =（4X72-240）/（4-2）=24

例2：一个水箱中装着螃蟹和牛蛙，共有头32，共有脚208，求螃蟹和牛蛙的数量。

求螃蟹时，假设全是牛蛙，则螃蟹数=（208-32X4）/（8-4）=20

求牛蛙时，假设全是螃蟹，则牛蛙数=（8X32-208）/（8-4）=12

4. 各类浓度问题

此类问题孩子主要的困难一是不知道从何下手，二是弄混了顺序，从而得出了错误的答案。

A、加水后稀释

【口诀】：

加水先求盐，盐完求盐水。

盐水减盐水，便是加水量。

例：有 40 千克浓度为 30%的盐水，在加入多少千克水后，浓度会变为 20%？

加水先求盐：原来含盐量为：40X30%=12（千克）

盐完求盐水： 12千克盐在 20%浓度下应有多少水，12/20%=60（千克）

盐水减盐水，便是加水量：最后将求出的总盐水量减去原来的盐水量，60-40=20（千克）

B、加盐后浓化

【口诀】：

加盐先求水，水完求盐水。

盐水减盐水，便是加盐量。

例：有40 千克浓度为 30%的盐水，加盐多少千克后，浓度变为 50%？

加盐先求水：原来含水为：40X（1-30%）=28（千克）

水完求盐水：含 28千克水在50%浓度下应有多少盐水，28/（1-50%）=56（千克）

盐水减盐水，便是加盐量：减去原来的盐水量，56-40=16（千克)

5. 路程问题

A、相遇问题（相向行驶，求相遇时间）

【口诀】：

相遇一刻，就是全程。

除以速度和，就把时间得。

例：甲乙两车从相距 120千米的两座城市相向而行，甲车的速度为 70千米/小时，乙车的速度为 50千米/小时，它们在经过多少时间后可以相遇？

相遇一刻，就是全程：即甲乙两车走过的全路程就是两地的距离—— 120千米。

除以速度和，就把时间得：即甲乙两人的总速度为两人的速度之和 70+50=120（千米/小时），所以相遇的时间就为 120/120=1（小时）

B、追击问题（先后行驶，求追上时间）

【口诀】：

慢鸟先飞，快的后追。

先走的路程，除以速度差，时间就求对。

例：一辆火车和一辆汽车启程前往一座城市，火车速度为 80 千米/小时，先走 2 小时后，汽车出发，速度为 100千米/小时，几时能追上？

先走的路程： 80X2=160（千米）

速度差：100-80=20（千米/小时）。

所以追上的时间为：160/20=8（小时）。

6. 和比问题（已知总和和各数比例，求各数）

【口诀】：

家要众人合，分家有原则。

分母比数和，分子自己的。

和乘以比例，就是该得的。

例：甲乙丙三数和为56，甲;乙:丙=1:2:4,求甲乙丙三数。

分母比数和，即分母为：1+2+4=7；分子自己的，则甲乙丙三数占和的比例分别为 1/7，2/7，4/7。

和乘以比例，所以甲数为 56X1/7=8，乙数为：56X2/7=16，丙数为：56X4/7=32。

7. 差比问题（已知差数和倍数，求各数）

【口诀】：

我的比你多，倍数是因果。

分子实际差，分母倍数差。

商是一倍的，乘以各倍数，两数便可得。

例：甲的岁数比乙大 24岁，甲岁数:乙岁数=8：5，求甲乙两人的岁数。

先求一倍的量，24/（8-5）=8

所以甲的岁数为：8X8=64，乙的岁数为：8X5=40。

8 . 工程问题

【口诀】：

工程总量设为 1，1除时间是工效。

单独做时工效是自己，一齐做时工效是众人效率和。

1减已做的便是没做的，没做的除以工效就是结果。

例：一项工程，甲公司单独做 需要花费8天完成，乙公司单独做需要 12天完成。甲乙公司同时做 4天后，由乙公司单独做，还需要几天完成？

工程总量设为 1，1除以时间就是工作效率：甲公司工作效率为1/8；乙公司工作效率为1/12

单独做时工作效率是自己的，一齐做时工作效率是众人的效率和：甲乙公司同时做 4天后完成量为（1/8+1/12）X4=5/6

1减去已经做的便是没有做的，没有做的除以工作效率就是结果：（1-5/6）/1/12=2天

9. 植树问题

孩子最容易算错的一类题目，主要问题就出在是否要减一上。

【口诀】：

植树多少棵，要问路如何？

直的减去 1，圆的是结果。

例 1：在一条长为 100 米的马路上植树，间距为 5 米，总共需要植树多少棵？

路是直的。所以植树量： 100/5-1=19（棵）。

例 2：在一条长为 100 米的圆形环岛周边植树，间距为 5米，总共需要植树多少棵？

路是圆的，所以植树量： 100/5=20（棵）

10. 盈亏问题

【口诀】：

全盈全亏，大减小；

一盈一亏，盈亏和。

除以分配差，结果就是分配量。

例 1：同学们分糖果，每人 5 个少 4 个；每人 4 个多 5 个。求有多少位同学和多少颗糖果？

一盈一亏，盈亏和：（5+4）/（5-4）=9（人），相应糖果数为 9X5-4=41（个）

例 2：挑夫背苹果。每人 150粒则多 180粒；每人 160粒则多 120粒，求有多少位挑夫和多少粒苹果？

全盈全亏，大减小：（180-120）/（160-150）=6（人）则苹果为 6X150+180=1080（粒）。

11. 牛吃草问题

【口诀】：

每牛每天的吃草量假设是份数 1，A头 B天的吃草量算出是几？M头 N天的吃草量又是几？

大减小，除以对应天数的差值，结果就是草的生长速率。原有的草量依此反推。

公式就是 A头 B天的吃草量减去 B天乘以草的生长速率。

将未知吃草量的牛分为两个部分：一小部分先吃新草，个数就是草的比率；

有的草量除以剩余的牛数就将需要的天数求知。

例：整个牧场上草长得一样密，一样快。27 头牛 6天可以把草吃完；23头牛 9天也可以把草吃完。问 21头多少天把草吃完。

每牛每天的吃草量假设是 1，则 27头牛 6天的吃草量是 27X6=162，23头牛 9天的吃草量是 23X9=207；

大的减去小的，207-162=45；二者对应的天数的差值，是9-6=3（天）结果就是草的生长速率。

所以草的生长速率是 45/3=15（牛/天）；原有的草量依此反推。

公式就是 A头 B天的吃草量减去 B天乘以草的生长速率：所以原有的草量=27X6-6X15=72（牛/天）。

将未知吃草量的牛分为两个部分：一小部分先吃新草，个数就是草的比率；这就是说将要求的 21 头牛分为两部分，一部分 15 头牛吃新生的草；剩下的 21-15=6 去吃原有的草，所以所求的天数为：

原有的草量/分配剩下的牛=72/6=12（天）

12. 年龄问题

【口诀】：

岁差不会变，同时相加减。

岁数一改变，倍数也改变。

抓住这三点，一切都简单。

例 1：小明今年 10 岁，妈妈今年36岁，在多少年后，妈妈的年龄的会是小明的 3倍？

岁差不会变：今年的岁数差点 36-10=26，到几年后仍然不会变。

已知差及倍数，转化为差比问题：26/（3-1）=13，几年后妈妈的年龄是 13X3=39 岁，小军的年龄是 13X1=13 岁？所以最终答案是 3 年后。

例 2：老王今年 33 岁，老刘今年 39 岁，当他们岁数的和是 82 岁时，两人各应该是多少岁？

岁差不会变，今年的岁数差39-33=6 几年后也不会改变。

几年后岁数和是 82，岁数差是 6，转化为和差问题。

则几年后，老王的岁数：（82-6）/2=38，老刘的岁数：（82+6）/2=44，所以答案是5 年后。

13. 余数问题

【口诀】：

余数有（N-1）个，最小是 1，最大是（N-1）。

周期变化时，不要看商，只看余。

例：如果时钟现在表示的时间是 20点整，那么分针旋转 889圈后是几点钟？

分针旋转一圈是 1 小时，旋转 24圈就是时针转 1圈，也就是时针回到原位。889/24的余数是 1，所以相当于分针向前旋转 1圈。

分针向前旋转 1个圈，相当于时针向前走 1个小时，即时针相当于是 20+1=21（点）。