八年级数学全等三角形证明条件归类

一、全等三角形证明条件归类：

从全等三角形证明的四种证明方法（边角边、角边角、角角边、边边边）来看：

①已知两边对应相等，第三个条件可以找已知两边的夹角对应相等 或 找第三边对应相等；

②已知两角对应相等，第三个条件可以找已知两个角的夹边对应相等 或 已知的两个角中的某个角的对应边相等；

③已知一边和一角对应相等，第三个条件可能是对应相等角的另一边对应相等 或 是另一角对应相等 。

综上：如何才能找到证明全等三角形的第三个条件呢？根据以上分析分为两种情况：

1、再找一组对应边相等；2、再找一组对应角相等。

二、对应边相等的情形：

1、公共边是第三个条件

例题1、如图，在△ABC 和 △ABD 中，AC = BD ，AD = BC ，求证 ： △ABC ≌ △ABD

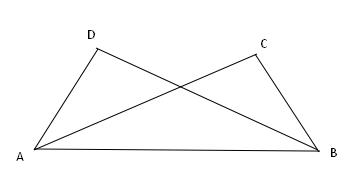
例题1图

证明：在 △ABD 和 △ BAC 中

∵ BD = AC ， BC = AD ， AB = BA （公共边）

∴ △ABC ≌ △ABD （SSS）

2、相等对应边 + 公共边的和 对应相等

例题2、如图，AB = CD ，AE = DF ， CE = FB ，求证 ：△ AEB ≌ △DFC

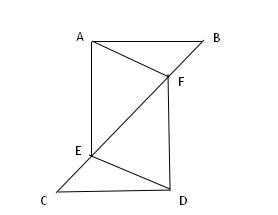
例题2图

证明：

∵ CE = FB ∴ CE + EF = EF + FB （即 CF = BE）

∵ AB = DC , AE = DF ，CF = BE

∴ △ AEB ≌ △DFC （SSS）

3、相等对应边 - 公共边的差 对应相等

例题3、如图，DF = CE , AD = BC , ∠D = ∠C ， 求证：△AED ≌ △BFC

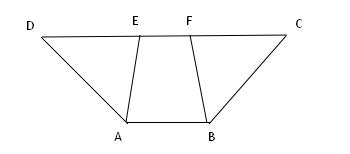
例题3图

证明：

∵ DF = CE ∴ DF - EF = CE - EF, 即 DE = CF

在 △AED 和 △BFC 中

∵ AD = BC , ∠D = ∠C ，DE = CF

∴ △AED ≌ △BFC （SAS）

4、等边三角形的三边相等（等腰三角形两腰相等）

例题4、如图， △ABC 和 △CDE 都是等边三角形 ，求证 ：△ACD ≌ △BCE

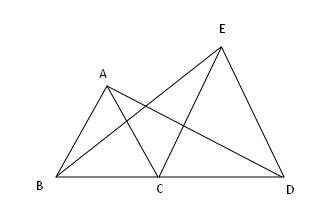
例题4图

证明：

∵ △ABC 和 △CDE 都是等边三角形

∴ AC = BC , CD = CE , ∠ACB = ∠DCE = 60°

∴ ∠ACB + ∠ACE = ∠DCE + ∠ACE 即 ∠BCE = ∠ACD

在 △BCE 和 △ACD 中

∵ BC = AC , ∠BCE = ∠ACD , CE = CD

∴ △BCE ≌ △ACD （SAS）

5、添加辅助线与对应的线段相等

例题5、如图，已知 AD 是 △ABC 中 ∠A 的角平分线，AC = AB + BD ，求证：∠B = 2∠C

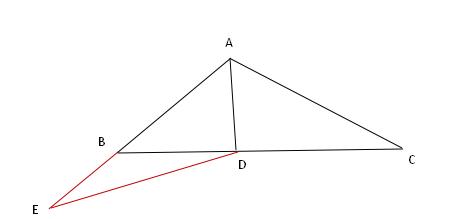
例题5图

证明：延长 AB 取点 E ，使 AE = AC , 连接 DE

∵ AD 平分 ∠BAC ∴ ∠EAD = ∠CAD

∵ AE = AC , AD = AD

∴ △AED ≌ △ACD （SAS）

∴ ∠E = ∠C

∵ AC = AB + BD ∴ AE = AB + BD

∵ AE = AB + BE ∴ BD = BE ∴ ∠BDE = ∠E

∵ ∠ABC = ∠E + ∠BDE ∴ ∠ABC = 2∠E ∴ ∠ABC = 2∠C

6、二次证全等找到对应的线段相等

例题6、如图，已知 ∠A = ∠D = 90° ，AE = DE , 求证 ： △ABC ≌ △DCB

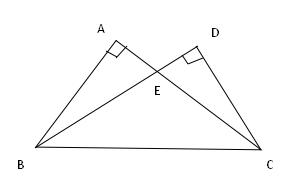
例题6图

证明：

∵ ∠A = ∠D ， AE = DE , ∠AEB = ∠DEC （对顶角相等）

∴ △AEB ≌ △DEC （ASA） ∴ EB = EC

∵ EB + ED = EC + AE ∴ DB = AC

在 Rt△ABC 和 Rt△DCB 中

∵ ∠A = ∠D = 90° ， AC = DB ， BC = CB （公共边）

∴ △ABC ≌ △DCB （HL）

三、对应角相等的情形：

1、公共角相等

例题7、如图，CA⊥BF 于点 A ，BE⊥CF 于点 E ，若 AC = BE ， 求证 ： △AFC ≌ △EFB

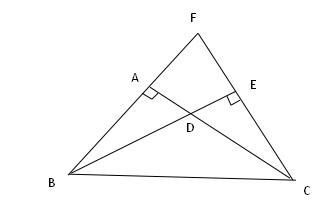
例题7图

证明：

∵ CA⊥BF ，BE⊥CF ∴ ∠CAF = ∠BEF= 90°

在 △AFC 和 △EFB 中

∵ ∠CAF = ∠BEF ，∠F = ∠F （公共角），AC = BE

∴ △AFC ≌ △EFB （AAS）

2、对顶角相等

例题8、如图，AE 和 BC 相交于点 M ，点 F 在 AM 上，∠CFM = ∠E ，BE = CF , 求证 ： △BEM ≌ △CFM

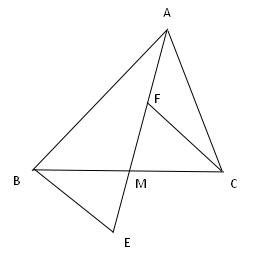
例题8图

证明略

3、平行线截得的同位角或内错角相等

例题9、如图，E, F 是四边形 ABCD 对角线 AC 上的两点，AF = CE ，DF = BE ，DF∥BE 。

求证：（1）△AFD ≌ △CEB ；（2）四边形 ABCD 是平行四边形吗？请说明理由。

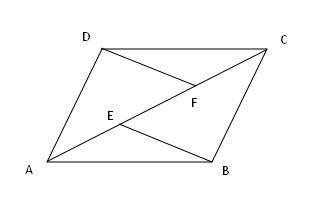
例题9图

证明：略

4、同角（或等角）的余角（或补角）相等

例题10、在 Rt△ABC 中，∠C = 90° ， CD⊥AB 于点 D ，

求证：（射影定理）

（1）AC^2 = AD • AB ;

（2）BC^2 = BD • AB ;

（3）CD^2 = BD • AD 。

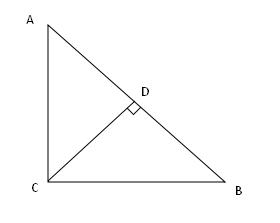
例题10图

思路：

找出图中的 3组 相似三角形，根据每组相似三角形对应边成比例来证明。

证明略。