中考数学，专题复习5：与圆有关的几何综合题

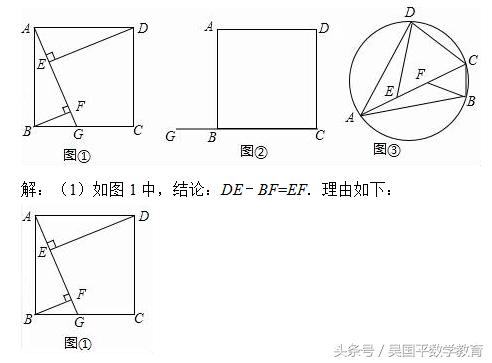
（1）如图①，四边形ABCD是正方形，点G是BC上的任意一点，BF⊥AG于点F，DE⊥AG于点E，探究BF，DE，EF之间的数量关系，第一学习小组合作探究后，得到DE﹣BF=EF，请证明这个结论；

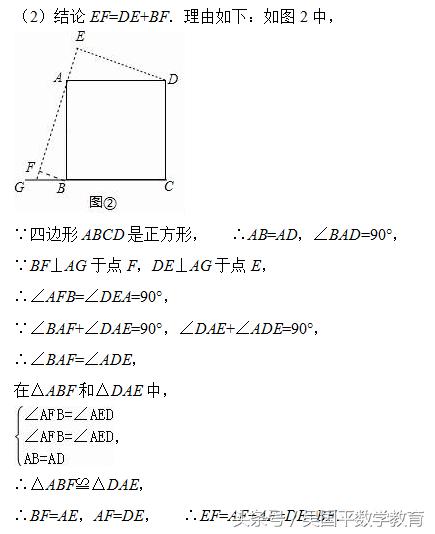
（2）若（1）中的点G在CB的延长线上，其余条件不变，请在图②中画出图形，并直接写出此时BF，DE，EF之间的数量关系；

（3）如图③，四边形ABCD内接于⊙O，AB=AD，E，F是AC上的两点，且满足∠AED=∠BFA=∠BCD，试判断AC，DE，BF之间的数量关系，并说明理由．

考点分析：

圆的综合题．

题干分析：

（1）如图1中，结论：DE﹣BF=EF．只要证明△ABF≌△DAE，即可解决问题．

（2）结论EF=DE+BF．证明方法类似（1）．

（3）如图3中，结论：AC=BF+DE．只要证明△ADE≌△BAF以及DE=EC即可解决问题．

解题反思：

本题考查圆综合题、正方形的性质、全等三角形的点评和性质、等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．