解析几何中的几何证明问题多出现在解答题当中，难度一般都较大，常常涉及线段的长度，角度，以及位置关系等问题。

解决圆锥曲线证明问题，注意依据直线，圆锥曲线，直线与圆锥曲线的位置关系等，通过代数恒等变形和化简计算进行证明，常见的证明方法有：

（1）证明三点共线，可以证明其中两段线段的斜率相等，也可以证明其中两个向量互相平行（共线）；

（2）证明两直线垂直，可以证明这两条直线的斜率之积等于负1，也可以证明这两直线所在的平面向量的数量积等于零；

（3）证明两共点点段相等，可以利用弦长公式证明这两线段长度相等，也可以证明公共点在线段的垂直平分线上。

一·套路

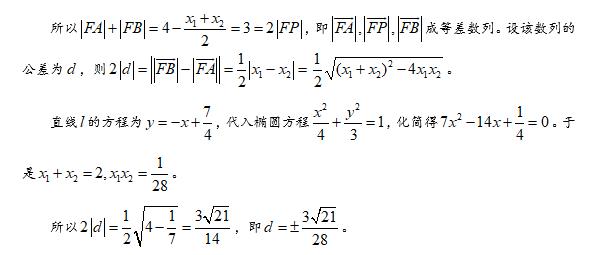
二·脑洞

本题考查圆锥曲线，涉及直线方程、直线与椭圆的位置关系、平面向量的运算、重心的性质、等差数列的性质等知识点，考查数形结合的思想和转化与划归的思想，考查逻辑推理能力和计算能力，属于难题。

法1，韦达定理，这已经是老生常谈了，还是熟悉的配方，还是熟悉的味道，可以参考前面文章，此处略过。

法2，点差法，点差法的结果是得到直线的斜率和线段中点坐标的关系，凡是涉及到中点弦问题，均可以尝试，这样可以避免韦达定理的繁琐计算。

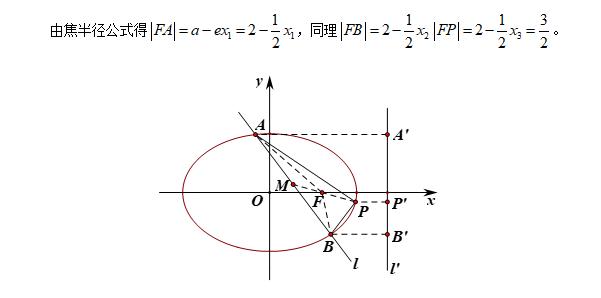
值得说明的是，本题中的焦半径可以直接利用椭圆的第二定义得到，遗憾的是目前高考弱化了第二定义，所以只能用两点的距离公式求解。我们将焦半径附录如下：

三·迁移

当然本题也不是什么创新试题，早在2013年的全国卷就考过一道类似的题目，只不过当年考的是双曲线，考的是等比数列而已。但是解题方法没有丝毫不同，由此可见，注重高考真题的训练是一件多么有价值的事。