数学经典试题

圆中的计算与证明是中学数学平面几何学习中的重点和难点，通常涉及到的图形多而复杂，辅助线的添加天马行空，计算与证明蜿蜒曲折.本文从一个不算难的题目着手，与大家一起探讨圆中的计算与证明破题之道.请看下面这个问题!

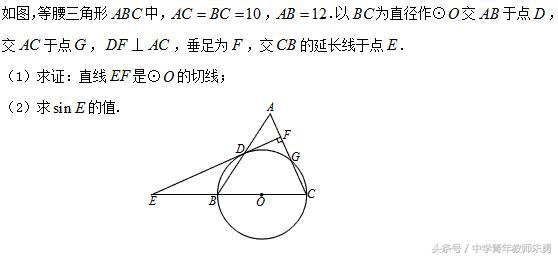
第一小问简单,下面介绍三个办法，不做过多累述.

方法一：抓等腰三角形三线合一，得中位线，利用平行线转化垂直关系.

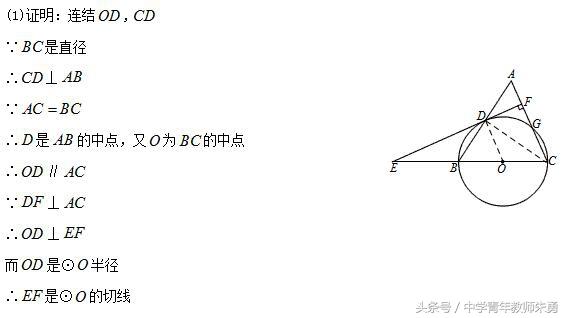
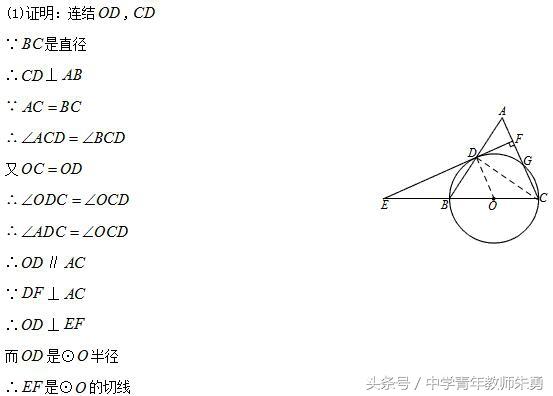
方法二：也是抓等腰三角形三线合一，得角平分线，利用平行线转化垂直关系.

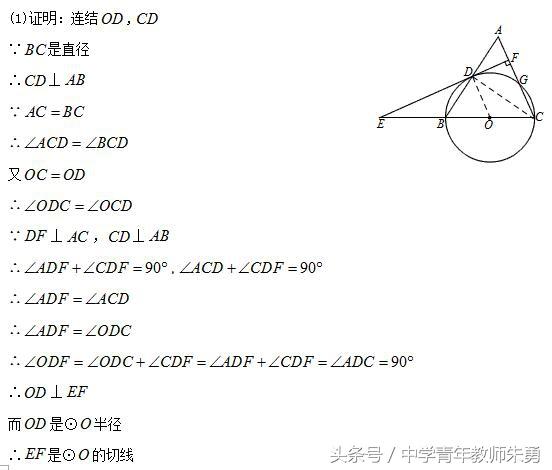
方法三：利用母子三角形转化角，抓余角性质.

下面重点说说第二小问，圆中的计算破题最主要是一个字“放”，放在不同图形当中就有不同身份，不同的身份就有不同的模型，不同的模型就有不同的解题策略！

方法一：放在直角三角形ODE中，抓勾股定理，弦切角定理，相似三角形性质.

方法二：放在直角三角形ODE中，抓切割线定理，勾股定理，相似三角形性质.

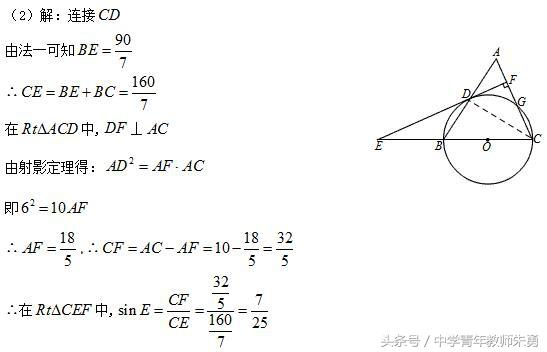
方法三：放在直角三角形CEF中，抓射影定理.

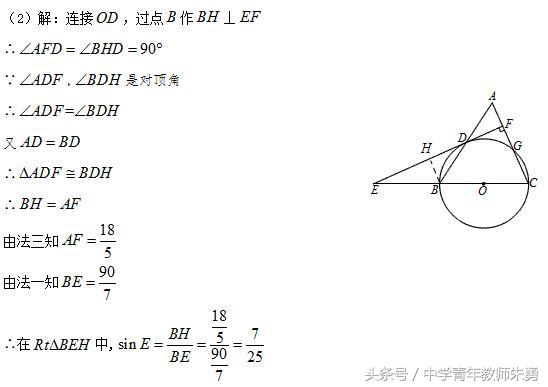
方法四：构造直角三角形BEH，抓平行线分线段成比例.

方法五：构造直角三角形BEH，抓全等三角形转化边.

方法六：构造直角三角形DEH，抓等面积法.

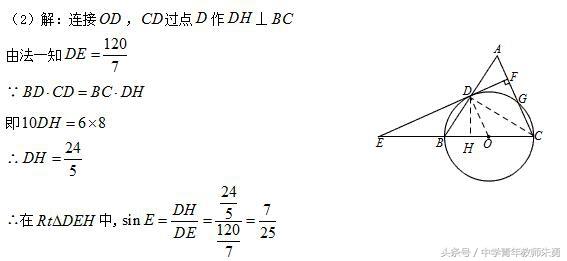
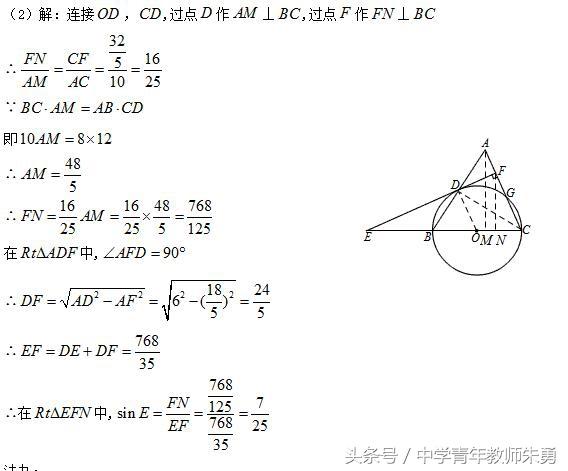
方法七：利用母子三角形转化角，抓等面积法，勾股定理或射影定理.

方法八：构造直角三角形EFN，抓平行线分线段成比例，勾股定理.

方法九：构造直角三角形EFN，利用母子三角形转化角，抓勾股定理.

方法十：利用余角公式转化角，转平行线分线段成比例.

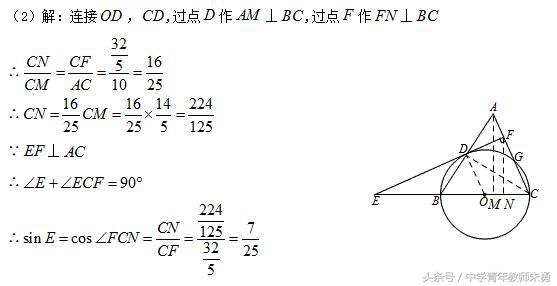
方法十一：利用平行线性质转化角，抓勾股定理.

方法十二：利用母子三角形转化角，抓等面积法和勾股定理.

方法十三：利用平行线性质转化角，抓割线定理.

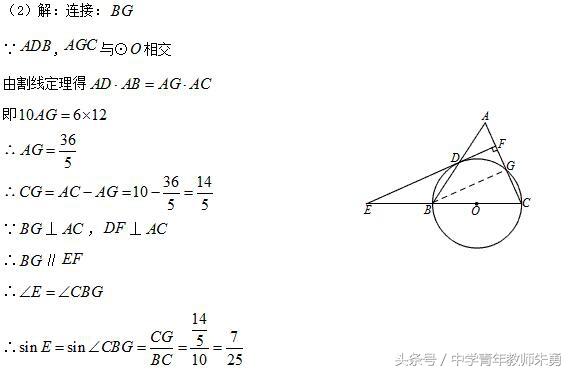
方法十四：利用母子三角形转化角，抓余弦定理.（初中阶段优尖生可以适当渗透！）