八年级数学常用辅助线添加方法 ~ 截长补短法

cc518学习网精品学习资料总目录

一、截长补短法：

题目中出现线段之间的和差倍分时，考虑截长补短；

截长补短的目的是把几条线段之间的数量关系转换为两条线段的等量关系。

二、典型例题：

例题1、如图，在 △ABC 中，∠1 = ∠2 ， ∠B = 2∠C ，求证： AC = AB + BD

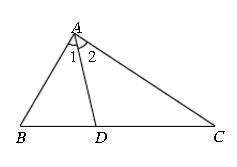
图1

证明：（截长法）如图，在线段 AC 上截取 AE = AB ，连接 DE

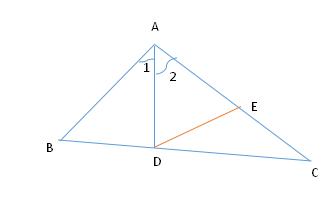
图2

∵ AB = AE , ∠1 = ∠2 ， AD = AD

∴ △ABD ≌ △AED

∴ BD = ED , ∠B = ∠AED , AB = AE

∵ ∠B = 2∠C ∴ ∠AED = 2∠C = ∠EDC + ∠C

∴ ∠EDC = ∠C ∴ ED = EC （等角对等边）

∵ AC = AE + EC

∴ AC = AB + BD （等量代换）

例题2、如图，在正方形 ABCD 中，E , F 分别为 DC ，BC 边上的点，且 ∠EAF = 45° ，连接 EF 。

求证： EF = BF + DE 。

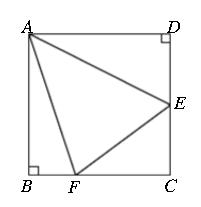
图3

证明：（补短法）如图，将 DE 补在 FB 的延长线上，使 BG = DE , 连接 AG

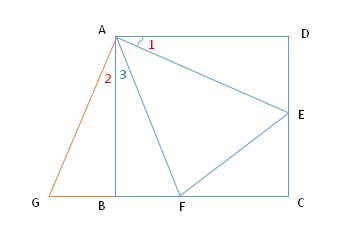
图4

∵ 在正方形 ABCD 中 有 AD = AB , ∠D = ∠ABG = 90° ， DE = BG

∴ △ADE ≌ △ABG ∴ ∠1 = ∠2 ， AE = AG

∵ ∠EAF = 45° ∠1 + ∠3 + ∠EAF = ∠DAB = 90°

∴ ∠1 + ∠3 = ∠2 + ∠3 = ∠GAF = 45° = ∠EAF

∵ AE = AG , ∠EAF = ∠GAF ， AF = AF

∴ △EAF ≌ △GAF ∴ EF = GF

∵ GF = BF + BG = BF + DE

∴ EF = BF + DE

例题3、如图，在 △ABC 中， ∠A = 90° ， AB = AC ，BD 平分 ∠ABC ，CE⊥BD 交 BD 的延长线于点 E 。

求证 ： CE = 1/2 BD 。

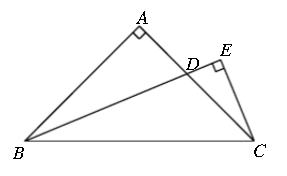
图5

证明：如图，延长 CE 交 BA 的延长线于点 F

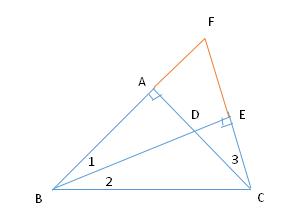
图6

∵ CE⊥BE ∴ ∠BEC = ∠BEF = 90°

∵ BD 平分 ∠ABC ∴ ∠1 = ∠2

∴ △BEC ≌ △BEF ∴ EC = EF

∵ ∠1 + ∠ADB = ∠3 + ∠EDC ， ∠ADB = ∠EDC （对顶角相等）

∴ ∠1 = ∠3

∵ AB = AC , ∠BAD = ∠CAF = 90° ， ∠1 = ∠3

∴ △ABD ≌ △ACF ∴ BD = CF = 2 CE

即 CE = 1/2 BD

三、拓展提高（作业题）

例题4、如图，在 △ABC 中，AM 是 BC 边上的中线 。

求证： AM < 1/2 ( AB + AC )

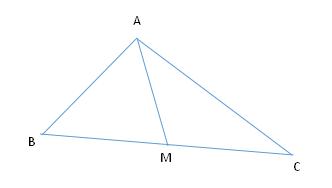
图7

例题5、如图，在 △ABC 中，∠ABC = 60° ，△ABC 的角平分线 AD , CE 相交于点 O 。

求证： AC = AE + AD 。

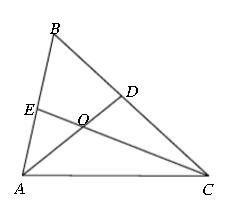
图8

例题5、如图，在梯形 ABCD 中，AD∥BC ，CE⊥AB 于点 E ，△BDC 为等腰直角三角形，∠BDC = 90° ，

BD = CD , CE 与 BD 相交于点 F ，连接 AF 。

求证： CF = AB + AF 。

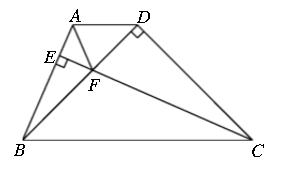
图9