高考数学，典型例题分析5：学会用双曲线性质解决问题

双曲线C：x2/a2-y2/b2=1（a＞0，b＞0）两条渐近线l1，l2与抛物线y2=﹣4x的准线1围成区域Ω，对于区域Ω（包含边界），对于区域Ω内任意一点（x，y），若（y-x-2）/（x+3）的最大值小于0，则双曲线C的离心率e的取值范围为　 　．

考点分析：

双曲线的简单性质．

题干分析：

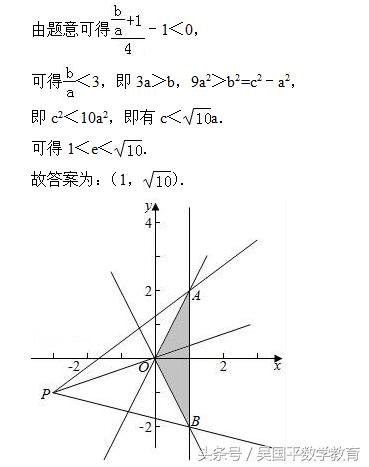
求得双曲线的渐近线方程和抛物线的准线方程，画出区域Ω，由（y-x-2）/（x+3）=（y+1）/（x+3）﹣1的几何意义是点（x，y）与点P（﹣3，﹣1）的斜率与1的差，结合图象，连接PA，可得斜率最大，再由双曲线的a，b，c关系和离心率公式计算即可得到所求范围．

解题反思：

高考对双曲线问题的考查多集中于选择与填空题，所以其高考中的热点问题也就多体现为：由定义求双曲线方程、求离心率及离心率的取值范围等。

双曲线是解析几何中的主干知识,在高考中也具有重要地位，通常涉及的双曲线考点主要有两个方面：一是双曲线的定义与性质的应用；二是双曲线与其他知识的交汇。

在高考中还经常考查双曲线独有的性质渐近线，以双曲线为载体考查其方程和性质。