中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用 “倍长中线法” 添加辅助线。
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而利用全等三角形的有关知识来解决问题的方法。
倍长中线法最重要的一点:延长中线一倍,完成 SAS 全等三角形模型的构造。
一、常用辅助线添加方法 ~ 倍长中线法
如图在 △ABC 中 , AD 是 BC 边上的中线:
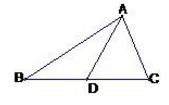
图1
方法一、延长 AD 到 E ,使 DE = AD ,连接 BE :
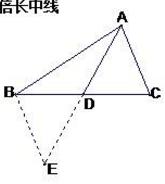
图2
方法二、间接倍长:
① 如图 作 CF⊥AD 于点 F ,作 BE⊥AD 的延长线于点 E ,
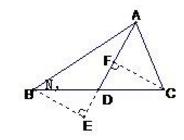
图3
② 如图 延长 MD 到 N 使 DN = MD ,连接 CN ,
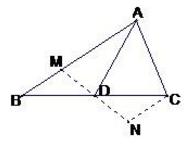
图4
二、典型例题
例题1、在 △ABC 中 ,AB = 5 , AC = 3 ,求中线 AD 的取值范围 。
思路:用方法一(利用三角形中三边关系确定中线范围)
例题2、已知在 △ABC 中,AB = AC , D 在 AB 上,E 在 AC 的延长线上,DE 交 BC 于点 F ,且 DF = EF ,
求证 : BD = CE
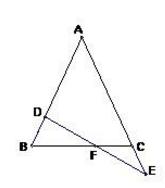
图5
证明: 过点 D 作 DG∥AC 交 BC 于点 G
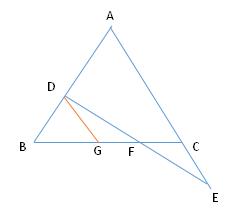
图6
∵ DG∥AC ∴ ∠GDF = ∠E , ∠DGB = ∠ACB
∵ DF = EF , ∠DFG = ∠EFC
∴ △DFG ≌ △EFC ∴ DG = CE
∵ AB = AC ∴ ∠B = ∠ACB
∴ ∠B = ∠DGB ∴ BD = DG = CE
例题3、已知在 △ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,且 BE = AC ,延长 BE 交 AC 于点 F ,
求证:AF = EF
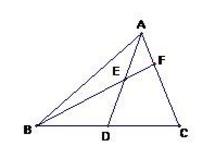
图7
证明:延长 AD 到点 G 使 ED = DG ,连接 CG
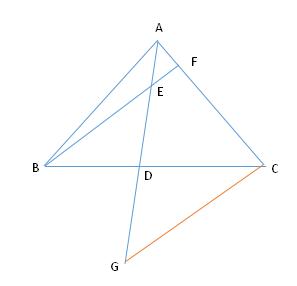
图8
∵ BD = DC , ED = GD , ∠BDE = ∠CDG
∴ △BDE ≌ △CDG ∴ BE = CG ,∠BED = ∠G
∵ BE = AC ∴ AC = CG ∴ ∠G = ∠CAG
∵ ∠BED = ∠AEF ∴ ∠AEF = ∠FAE
∴ AF = EF
三、拓展提高(作业题)
例题4、如图,在 △ABC 中,AB ≠ AC ,D , E 在 BC 上,且 DE = EC , 过点 D 作 DF∥BA ,交 AE 于点 F ,DF = AC 。
求证: AE 平分 ∠BAC
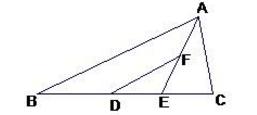
图9
 加载中,请稍侯......
加载中,请稍侯......
精彩评论