中考数学，专题复习1：几何变换综合题

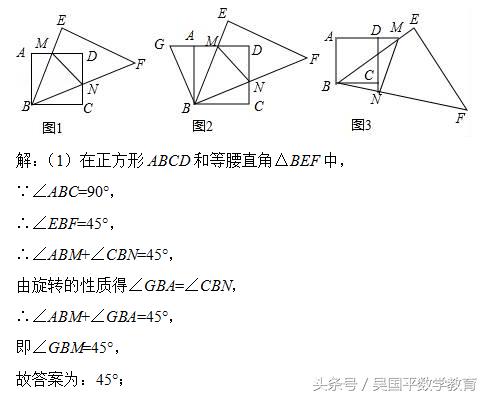
将一块正方形和一块等腰直角三角形如图1摆放．

（1）如果把图1中的△BCN绕点B逆时针旋转90°，得到图2，则∠GBM= ；

（2）将△BEF绕点B旋转．

①当M，N分别在AD，CD上（不与A，D，C重合）时，线段AM，MN，NC之间有一个不变的相等关系式，请你写出这个关系式： ；（不用证明）

②当点M在AD的延长线上，点N在DC的延长线时（如图3），①中的关系式是否仍然成立？若成立，写出你的结论，并说明理由；若不成立，写出你认为成立的结论，并说明理由．

考点分析：

几何变换综合题．

题干分析：

（1）由旋转的性质得∠GBA=∠CBN，于是得到∠ABM+∠GBA=45°，即可得到结论；

（2）①根据旋转的性质得到∠GAB=∠C=90°，AG=CN，BG=BN，∠ABG=∠CBN，得到D，A，G三点共线，根据全等三角形的性质得到GM=MN，于是得到结论；

②在AM上截取AG，使得AG=CN，连结BG；根据正方形的性质得到AB=BC，∠A=∠BCN=90°，根据全等三角形的性质得到BG=BN，∠ABG=∠NBC，根据全等三角形的性质即可得到结论．