八年级数学三角形中的有关计算与证明

1、 如图 在 △ABC 中 ，AB = 4，AC=2，D 是 BC 中点，若 AD 是整数，求 AD 的长度？

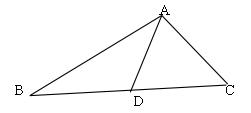
第1题图

解：延长AD到E,使AD=DE

∵ AB-BE＜AE＜AB+BE 即 1＜AD＜3

∴ AD = 2 。

2、 如图，在△ABC 中 ， D 是 AB 的中点，∠ACB=90°，求证： CD = 1/2 AB 。

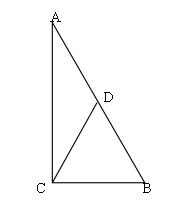
第2题图

证明：延长CD 到 P 点，使 D为 CP 的中点，连接 PA 和 PB ，则四边形 PACB 为矩形；

由矩形的性质可知 矩形的对角线相等且互相平分，所以 CD = 1/2 AB 。

推论：直角三角形斜边上的中线等于斜边的一半。

3、如图，在五边形 ABCDE 中 ，BC = DE，∠B = ∠E，∠C = ∠D，F 是 CD 中点，求证：∠1=∠2 。

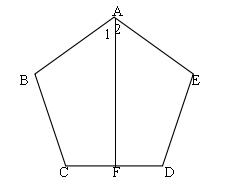
第3题图

证明：

连接 BF 和 EF ∴ △BCF ≌ EDF (SAS) ∴ BF=EF, ∠CBF=∠DEF

连接 BE ∴ ∠EBF=∠BEF

∵ ∠ABC=∠AED ∴ ∠ABE=∠AEB

∴ AB=AE ∴ △ABF ≌ △AEF ∴ ∠BAF=∠EAF (∠1=∠2)。

4、如图，在 △ABC 中 ∠1=∠2，CD = DE，EF//AB，求证：EF = AC 。

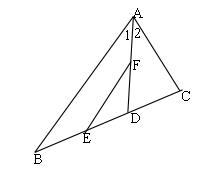
第4题图

证明：

过点 C 作 CG∥EF 交AD 的延长线于点 G，由CG∥EF，可得 ∠EFD＝∠CGD ；

∴ △EFD ≌ △CGD EF＝CG ∴ △AGC为等腰三角形，GC = AC 。

易证 △DFE ≌ △DGC （AAS） ∴ GC = EF = AC 。

5、在 △ABC 中， 已知 AD 平分 ∠BAC，AC = AB + BD，求证：∠B = 2∠C 。

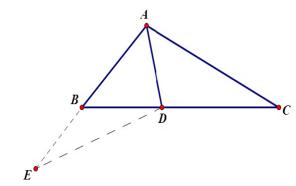
第5题图

证明：

延长 AB 取点 E，使 AE ＝ AC，连接 DE

∴ △AED ≌ △ACD （SAS） ∴ ∠E = ∠C

∵ AC = AB + BD ∴ AE = AB + BD = AB + BE ∴ BD = BE

∴ △BED 为等腰三角形

∴ ∠B = 2∠C （三角形外角和定理） 。

6、如图，已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE 。

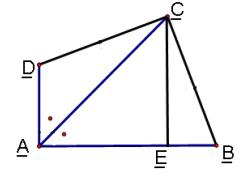
第6题图

证明：

在AE上取点 F，使 EF＝ EB，连接 CF

∵ CE⊥AB ∴ △CEB ≌ △CEF ∴ ∠B＝∠CFE

∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°

∴∠D＝∠CFA ∴△ADC≌△AFC（SAS）

∴ AD＝AF ∴ AE＝AF＋FE＝AD＋BE

7、如图，在四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，点 E 在 AD上 。

求证：BC = AB + DC 。

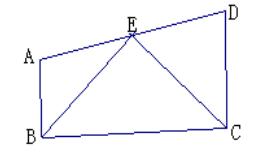
第7题图

证明：

在BC上截取BF=AB，连接EF

∴⊿ABE ≌ ⊿FBE（SAS） ∴∠A = ∠BFE ∴ ∠D = ∠CFE

∴ ⊿DCE ≌ ⊿FCE（AAS） ∴ CD = CF ∴ BC = BF+CF = AB + CD 。

8、如图，已知：AB=CD，∠A=∠D，求证：∠B=∠C。

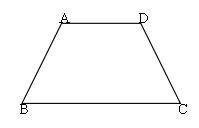
第8题图

证明：

E点是射线 BA,CD 的交点，则：△AED 是等腰三角形 。

∴AE=DE ∴ BE = CE (等量加等量，或等量减等量）

∴△BEC是等腰三角形 ∴∠B=∠C。

9、如图，点 P 是 ∠BAC平分线 AD 上一点，AC > AB，求证：PC - PB < AC - AB 。

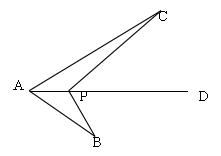
第9题图

证明：

在AC上取点E， 使AE＝AB；

∴△EAP≌△BAP ∴PE＝PB PC＜EC＋PE ∴ PC＜（AC－AE）＋PB

∴ PC－PB＜AC－AB 。

10、如图， 已知 ∠ABC =3∠C，∠1=∠2，BE⊥AE，求证：AC - AB= 2BE 。

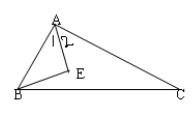
第10题图

证明：

在AC上取一点D，使得∠DBC=∠C

∵∠ABC=3∠C ∴∠ABD=∠ABC-∠DBC = 3∠C - ∠C=2∠C；

∵∠ADB=∠C+∠DBC=2∠C; ∴AB=AD ∴AC – AB =AC-AD=CD=BD

在等腰△ABD 中，点 E 一定在直线 BD 上，

在等腰△ABD中，∴BD=2BE

∵BD=CD=AC-AB ∴AC-AB= 2BE 。

11、如图，已知，点 E 是 AB 的中点，AF = BD，BD = 5，AC = 7，求 DC 的长度。

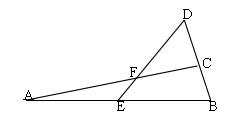
第11题图

证明：

∵ 作 AG∥BD 交 DE 延长线于 点 G

∴△AGE ≌ △BDE ∴ AG = BD = 5

∴△AGF∽△CDF AF=AG=5 ∴DC = CF = 2 。

12、如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M。

（1）求证：MB=MD，ME=MF ；

（2）当E、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由。

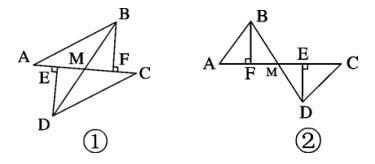
第12题图

证明：

（1）连接BE，DF

∵DE⊥AC于E，BF⊥AC于F， ∴∠DEC=∠BFA=90°，DE∥BF，

在Rt△DEC和Rt△BFA中， ∵AF=CE，AB=CD，

∴Rt△DEC≌Rt△BFA（HL）， ∴DE=BF．

∴四边形BEDF是平行四边形． ∴MB=MD，ME=MF；

（2）连接BE，DF

∵DE⊥AC于E，BF⊥AC于F， ∴∠DEC=∠BFA=90°，DE∥BF，

在Rt△DEC和Rt△BFA中， ∵AF=CE，AB=CD， ∴Rt△DEC≌Rt△BFA（HL），

∴DE=BF． ∴四边形BEDF是平行四边形． ∴MB=MD，ME=MF。

13、已知：如图，DC∥AB，且DC=AE，E为AB的中点 。

（1）求证：△AED ≌ △EBC；

（2）观看图前，在不添辅助线的情况下，除△EBC外，请再写出两个与△AED的面积相等的三角形，

（直接写出结果，不要求证明）。

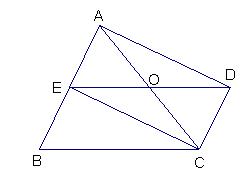
第13题图

证明：

（1）∵DC∥AB ∴∠CDE＝∠AED ∵DE＝DE，DC＝AE

∴△AED≌△EDC ∵E为AB中点 ∴AE＝BE

∴BE＝DC ∵DC∥AB ∴∠DCE＝∠BEC ∵CE＝CE

∴△EBC ≌ △EDC ∴△AED ≌ △EBC

（2）略 。

14、如图，△ABC中，∠BAC=90°，AB=AC，BD 是 ∠ABC 的平分线，BD的延长线垂直于过C点的直线于E，直线 CE 交 BA 的延长线于点 F，求证：BD=2CE。

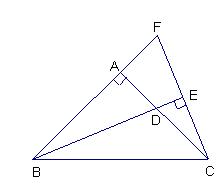
第14题图

证明：

易证 ∠FCA = ∠DBA

∴ △AFC ≌ △ADB ∴ FC = BD

再证 △BFE ≌ △BCE （或 △FBC 为等腰三角形）

∴ EF = EC ∴ BD = 2CE

15、如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC。

求证：（1）EC=BF；（2）EC⊥BF 。

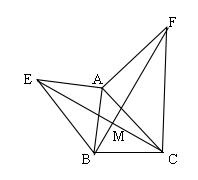
第15题

证明：

（1）△ABF ≌ △AEC（SAS）；

（2）如图，根据（1）知 △ABF ≌ △AEC，

∴ ∠AEC=∠ABF， 在△BDM中，∠BMD=180°-∠ABF-∠BDM=180°-90°=90°，

∴ EC⊥BF 。

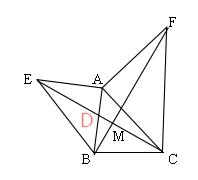
第15题答图