一·套路

二·脑洞

1. 本题考查直线与抛物线的位置关系，涉及直线方程，角平分线，韦达定理等知识点，考查设而不求，分类讨论，以及数形结合的思想，属于中档题。

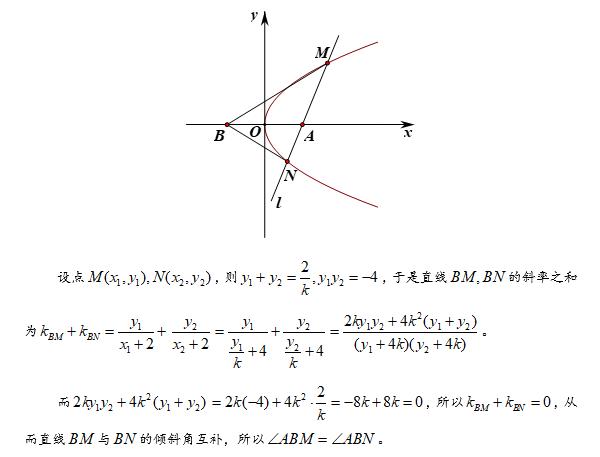
2. 法1，利用点斜式设直线的方程，但要注意讨论直线斜率不存在的情况，避免因不严谨而失分。坐标轴作为角平分线等价于两直线的倾斜角互补，进而等价于两直线的斜率互为相反数，这便是法1的核心解题思路。

3. 法2，反设直线方程，这样设直线方程有两个好处：一是不用讨论直线斜率不存在的情况；二是联立方程，计算更为简洁。当然法2与法1本质上都是一样的，都是利用韦达定理转化为两直线的斜率互为相反数来求解。

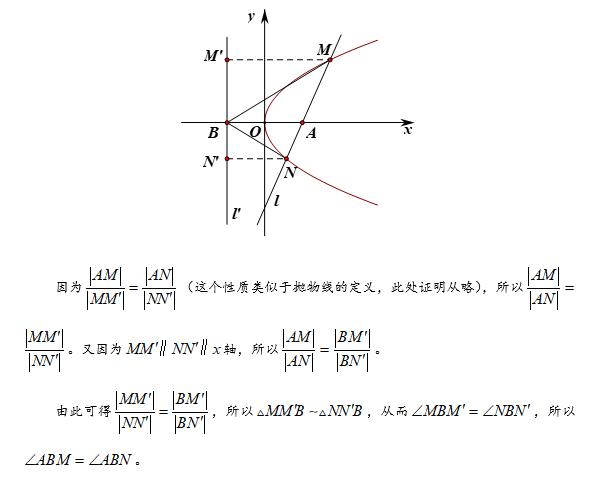
4. 法3，通过角平分线性质来解答，也即是角平分线上的点到角的两边的距离相等。由于原点在角平分线上，因此，选择原点可以大大减少计算量。直接计算得到两个距离相等似乎不太容易，因此，本题采用分析法来证明。

5. 法4，由于解析几何也是几何，当然可以采用平面几何的方法来进行解答，有些题目用平面几何的方法解答甚至会受到奇效。值得说明的是，本题第二问的结论还可以推广至一般情况，在此不作赘述。

6. 最后，本题还可以借助平面向量的夹角公式来进行解答，感兴趣的可以自行尝试。

三·迁移

2018年高考数学全国1卷，真的是平平无奇，所有试题几乎都没有特色和亮点。下面我们给出2015年全国课标1卷的20题，仔细对比会发现，二者几乎雷同。三年前才考过，今年就迫不及待地又考，就更加凸显命题者有偷懒的嫌疑。

当然，这也意味着，将来高考复习仍然要以基础知识为核心，以典型考题为重点，而不必一味地追求创新试题和特色试题，最后得不偿失。