函数的最值是函数的重要性质之一，在高考中也经常考查，并且具有相当的难度。求函数的最值的方法非常之多，如分离常数法、判别式法、反函数法、数形结合法、均值不等式法、导数法等等。本讲针对2018年高考全国1卷理科数学地16题作简单分析。

一·套路

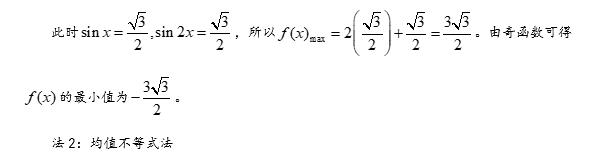
二·脑洞

本题借助三角函数为载体，考查函数的最值，属于难题。解答的思路是，首先利用三角函数的周期性与奇偶性，将函数的简化到一个具体的区间上来讨论，然后再根据不同的思维模式，给出三种不同的解题方法。

1. 第一种是利用导数法求解，这种解法最容易理解，也最容易想到。通过求导，判断函数的单调性，进而求得函数的最小值点，得到相应的三角函数值，带回原函数即可求得最小值。

2. 第二种解法是构造均值不等式求解，有一定的难度。多元均值不等式在构造技巧上具有一定的难度，加上高考数学中鲜有涉及，所以不易联想到。但对成绩优秀的，或者参加过竞赛的学生，完全可以掌握这种方法。值得注意的是，均值不等式是解决最值问题常用工具，但需要注意其构造技巧。

3. 第三种方法是利用高等数学中的琴生不等式求解。琴生不等式是函数凹凸性的重要结论，它在证明不等式和求最值中具有广泛的作用。近年来，借助高等数学背景考查高中数学内容越来越成为共识，因此了解一些高等数学的结论对解题无疑是如虎添翼。

下面给出本题函数的图象，从图象上可以直观感受其性质：

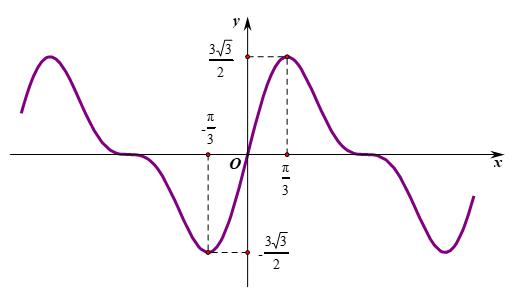
f（x）的图象

三·迁移

下面给出一道类似的高考试题作为练习：

事实上，函数关于（0，1）点中心对称，所以最大值与最小值关于1对称，从而M+m=2。其图象如下：

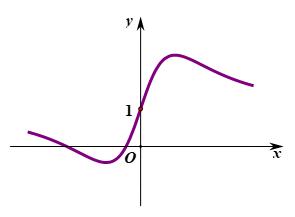
f（x）的图象