1. 在高考数学中，导数最为压轴题已经算不得什么奇观，就连一向以数列压轴的浙江卷，今年也一改常态，加入了导数的行列。

2. 导数压轴题大致可以分为以下几种类型：（1）考查函数的单调性，极值与最值；（2）考查函数零点的讨论；（3）考查不等式的证明；（4）考查不等式恒成立或有解，求参数的取值范围等等。

3. 解决导数压轴题的常规思路无非是构造函数，分类讨论，数形结合，转化与划归。当然，毕竟是压轴题，具有一定的区分度，其思维层次和计算量都很大，要正确解答，也并非说得那么云淡风轻。下面就2018年高考全国1卷数学理科21题作简单分析。

一·套路

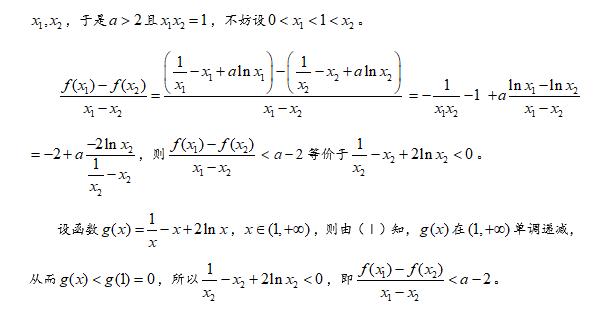
二·脑洞

1. 本题是今年全国1卷理科数学的压轴题，考查导数的综合应用，涉及函数的单调性，函数的极值，以及不等式的证明等知识点，属于难题。

2. 本题第（1）问，讨论含参函数的单调性，没有什么可说的，直接求导后，对参数进行分类讨论，从而得出结论。

3. 本题第（2）问，考查不等式的证明，我们给出3中方法。前两种方法将结论进行等价转化，构造新函数，结合第（1）问，利用函数的单调性加以证明。事实上，这两个方法本质上是一样的，差别仅仅在于变量的选取不同而已。另外本题属于递进式设问，设计十分巧妙，构造的新函数恰好可以利用第（1）问的结论，从而使得题目更加紧凑，也大大降低了运算量。

4. 第三种方法借助对数平均不断等式，堪称秒杀。值得说明的是，对数平均不等式不能直接使用，需要先进行证明，其证明过程如下：

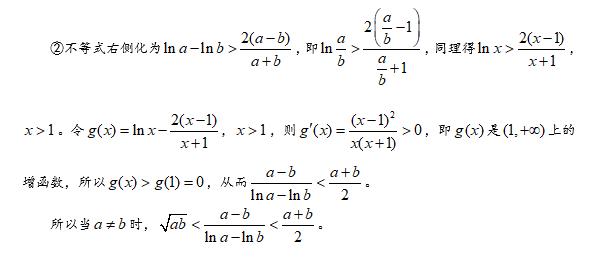
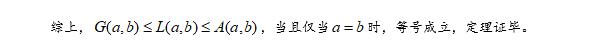
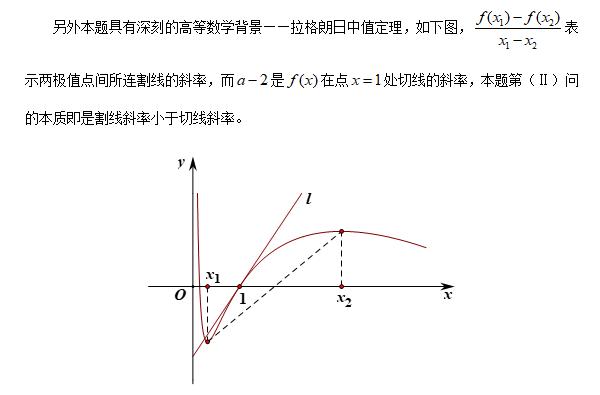
三·迁移

最后，本题真的算不上匠心独具的高考试题，因为早在2011年，湖南高考数学文科压轴题就是考的这个东东，我们作为变式附录如下，仔细对比，有没有一种被抄袭的感觉？