基本图形分析法：帮你分析角平分线和垂线的组合图形（十一）

【分析方法导引】

当几何问题中，出现了角平分线和向角平分线所作的垂线的时候，就要想到可应用等腰三角形中重要线段的基本图形进行证明。

若角平分线的垂线没有过角的顶点时，可直接将角平分线的垂线延长到与角的两边相交，构成等腰三角形中重要线段的基本图形，然后再应用一次轴对称型全等三角形来完成分析。

若角平分线的垂线经过角的顶点时，则应将角平分线的垂线平行移动，使它离开角的顶点，然后再与角的两边相交构成等腰三角形中的重要线段的基本图形。

例18 如图3-184，已知：△ABC中，AD是高，P是AD上的任一点，BP、CP的延长线分别交AC、AB于E、F。求证：∠EDP=∠FDP。

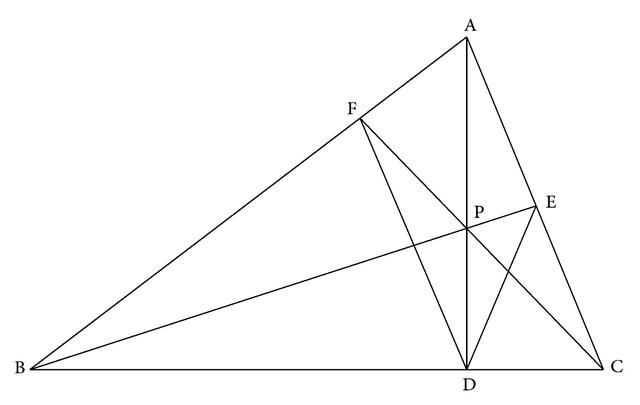
图3-184

分析：本题要证∠EDP=∠FDP，即DP是∠EDF的角平分线。而条件中出现AD是高，也就是BC是角平分线DP的垂线，从而就可构成一个等腰三角形的基本图形。这个等腰三角形应是由角平分线的垂线和角的两边相交得到，而现在图形中由于角平分线DA的垂线BC是经过∠EDF的顶点D的，因此等腰三角形退化成一个点，即等腰三角形消失。这样要作出等腰三角形，就必须要使这条角平分线的垂线离开角的顶点，而要使这条垂线既离开顶点又要保持与角平分线垂直，那也就是将BC平移。而在平移过程中，只要一离开D点就可以在与角的两边相交后出现等腰三角形，所以在这个平移过程中能够得到的等腰三角形显然就可以有无数多个，因此，问题就成为要选择一个恰当的位置或者也就是选取一个恰当的点作BC的平行线。由于A是条件中给出的已知三角形的顶点，所以我们可选择过A作平行线，也就是过A作MN⊥AD交DE、DF的延长线于M、N（如图3-185），那么△DMN必定是等腰三角形，而要证明∠MDA=∠NDA，也就可以转化要证明AM=AN。而条件BC⊥AD和所作MN⊥AD，可得MN∥BC。这样AN和DB就是两条平行线段，且它们四个端点两两的连线在F点相交，从而可应用由三角形外一条边的平行线所得到的平行线型相似三角形进行证明（如图3-186）。也就是由AD∥DB，可得△AFN∽△BFD，AN/BD=AF/BF，从而有AN=AE/BF·BD。根据同样的道理还可得AM=AE/CE·CD。这样要证明AM=AN，就可以转化为证AE/CE·CD=AF/BF·BD，将这个关系式中的项都移到等式的一边去，也就是要证AE/CE·CD/BD·BF/AF=1.显然这是西瓦定理结论的表达式，所以由△ABC内AD、BE、CF三线共点于P，那么直接应用西瓦定理就可以证明上述性质。

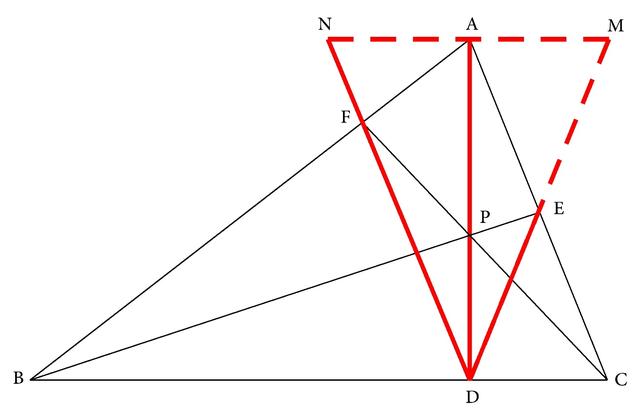
图3-185