中考数学，专题复习98：四边形相关的综合题

提出问题：

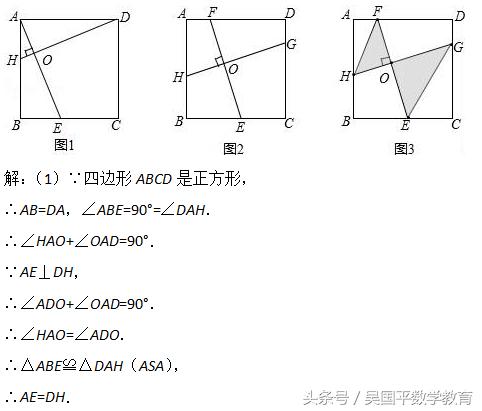
（1）如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE⊥DH于点O，求证：AE=DH；

类比探究：

（2）如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；

综合运用：

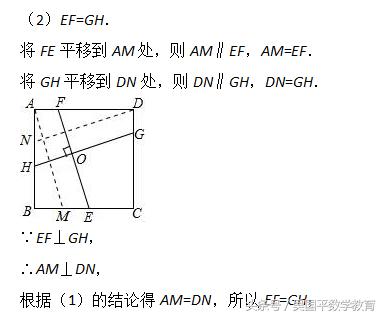
（3）在（2）问条件下，HF∥GE，如图3所示，已知BE=EC=2，EO=2FO，求图中阴影部分的面积．

考点分析：

四边形综合题．

题干分析：

（1）由正方形的性质得AB=DA，∠ABE=90°=∠DAH．所以∠HAO+∠OAD=90°，又知∠ADO+∠OAD=90°，所以∠HAO=∠ADO，于是△ABE≌△DAH，可得AE=DH；

（2）EF=GH．将FE平移到AM处，则AM∥EF，AM=EF，将GH平移到DN处，则DN∥GH，DN=GH．根据（1）的结论得AM=DN，所以EF=GH；

（3）易得△AHF∽△CGE，所以AF/CE=FH/EG=FO/OE=1/2，由EC=2得AF=1，过F作FP⊥BC于P，根据勾股定理得到EF的值，因为FH∥EG，所以FO/FE=HO/HG，根据（2）①知EF=GH，所以FO=HO，再求得三角形FOH与三角形EOG的面积相加即可．