二次函数图象中的面积问题

二次函数综合题中，常常会考面积相关的问题．

通常解决此类问题的关键是用未知数表示出图形的面积，再解决问题．

因此，第一步一般需要设出动点坐标（或用条件中的动点坐标），再选择适当的方式求图形的面积（三角形或四边形），然后用未知数表示出需要求的线段的长度，再得出结论．

常用求面积方法：

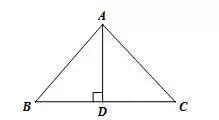
①直接法求三角形面积．如图所示，△ABC中AD为边BC上的高，则S△ABC＝1/2BC·AD．

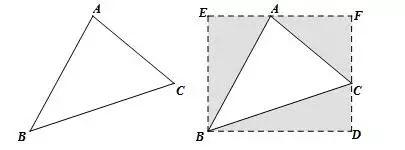
②补全法求三角形面积．如图所示，S△ABC＝S矩形BDFE－ S△ABE－ S△ACF－ S△BCD．

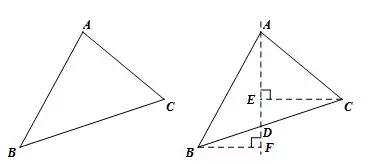
③分割法求三角形面积．如图所示，S△ABC＝S△ABD＋S△ACD＝AD·BF＋AD·CE＝AD·(BF＋CE)．

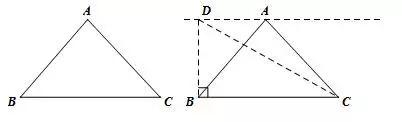
④平移法求三角形面积．如图所示，过点A作AD∥BC，则S△ABC＝S△BCD．

当一个三角形（或其他多边形）的形状或大小发生变化时，产生面积变化．选择合适的方法，利用已知条件求出变化过程中该三角形（或其他多边形）的面积．

【典型例题】

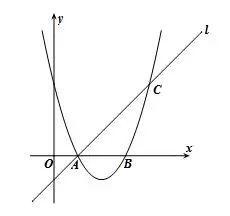
1．如图，已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．

（1）求抛物线的解析式；

（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；

（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．

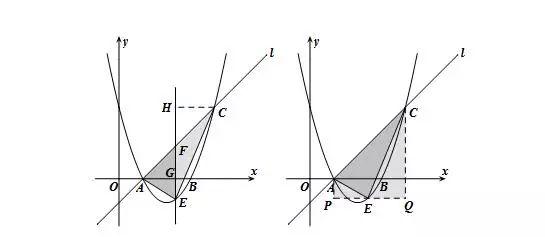
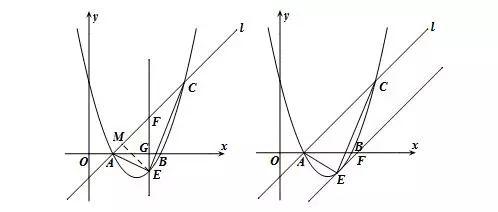
此类问题非常常见，不难掌握，希望大家灵活选择适当的方法．