中考数学图形的相似专题训练

一、选择题

1、如果两个相似三角形的面积比是 1:4 ，那么它们的周长比是 （D）。

A、1 : 16 B、1 : 4 C、1 : 6 D、1 : 2

2、已知 △ABC∽△DEF ，若 △ABC 与 △DEF 的相似比为 3/4 ，则 △ABC 与 △DEF 对应中线的比为 （A）。

A、3 : 4 B、4 : 3 C、9 :16 D、16 : 9

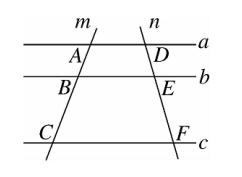
3、如图，已知直线 a∥b∥c ，直线 m 交直线 a, b , c 于点 A,B,C , 直线 n 交直线 a, b , c 于点 D , E, F ,

若 AB/BC = 1/2 ，则 DE/EF 的值为 （B）。

A、1/3 B、1/2 C、2/3 D、1

图（1）

4、如图，在 △ABC 中，DE∥BC ，AD/AB = 1/3 ，BC = 12 ，则 DE 的长是 （B）。

A、3 B、4 C、5 D、6

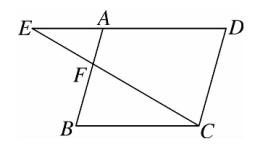
5、如图，点 F 在平行四边形 ABCD 的边 AB 上，射线 CF 交 DA 的延长线于点 E ，在不添加辅助线的情况下，

与 △AEF 相似的三角形有 （C）。

A、0 个 B、1 个 C、2 个 D、3 个

图（2）

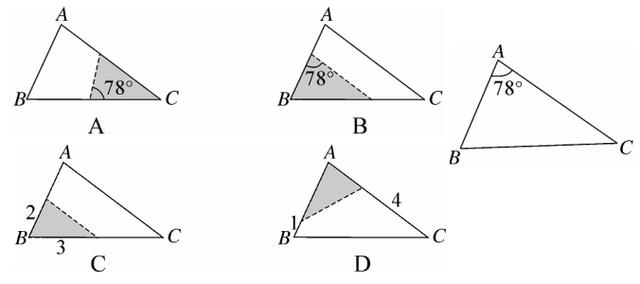
6、如图，△ ABC 中，∠A = 78°，AB = 4 ，AC = 6 。将 △ABC 沿图示中的虚线展开，剪下的阴影三角形与原三角形不

相似的是 （C）。

图（3）

7、如图，在平面直角坐标系中，已知点 A（-3,6），B（-9，-3），以原点 O 为位似中心，相似比为 1/3 ，把 △ABO 缩小，则

点 A 的对应点 A' 的坐标是 （D）。

A、（-1,2） B、（-9,18） C、（-9,18）或 （9，-18） D、（-1,2）或 （1，-2）

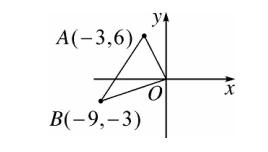
图（4）

8、如图，在直角梯形 ABCD 中，AD∥BC ，∠ABC = 90°，AB = 8 ，AD = 3 ，BC = 4 ，点 P 为 AB 边上一动点，若 △PAD 与

△PBC 是相似三角形，则满足条件的点 P 的个数是 （C）。

A、1个 B、2 个 C、3个 D、4 个

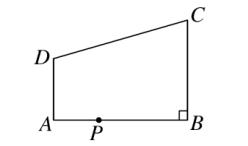
图（5）

解析：

解析图（1）

9、如图，点 E，F 分别在棱形 ABCD 的边 AB，AD 上，AE = DF ，BF 交 DE 于点 G ，延长 BF 交 CD 的延长线于 H ，

若 AF/DF = 2 , 则 HF/BG 的值为 （B）。

A、2/3 B、7/12 C、1/2 D、5/12

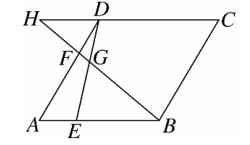
图（6）

解析：

解析图（2）

10、如图，在四边形 ABCD 中，AD∥BC ，∠ABC = 90°，E 是 AB 上一点，DE⊥CE 。若 AD = 1 ，BC = 2 ，CD = 3 ，

则 CE 与 DE 的数量关系正确的是 （B）。

A、CE = √3 DE B、CE = √2 DE C、CE = 3 DE D、CE = 2 DE

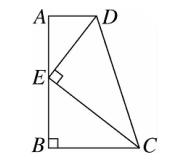
图（7）

解析：

解析图（3）

二、填空题

11、若 x : y = 1 : 3 ，2y = 3z ，则 (2x + y ) ： （z - y ） = - 5 。

12、如图，已知 ∠A = ∠D ，要使 △ABC∽△DEF ，还需添加一个条件，你添加的条件是 AB∥DE （答案不唯一）

（注：只需写一个条件，不添加辅助线和字母）。

图（8）

13、在平行四边形 ABCD 中，M ， N ，是 AD 边上的三等分点，连接 BD ，MC 相交于 O 点 ，则 S△ODM ： S△OBC = 4/9 或 1/9。

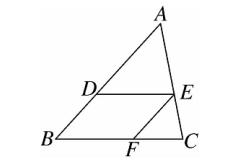
14、如图，在 △ABC 中，点 D，E，F 分别在 AB，AC，BC 上，DE∥BC ，EF∥AB 。

若 AB = 8 ， BD = 3 ，BF = 4 ，则 FC 的长为 12/5 。

图（9）

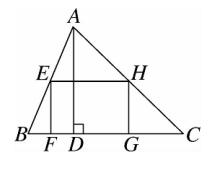
15、如图，矩形 EFGH 内接于 △ABC ，边 FG 落在 BC 上，若 AD⊥BC ，BC = 3 ，AD = 2 ，EF = 2/3 EH ，则 EH 的长为 3/2 。

图（10）

解析：

解析图（4）

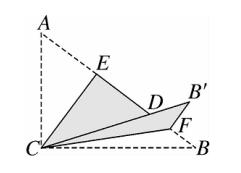
16、如图，Rt△ABC 中，∠ACB = 90°，AC= 3 ，BC = 4 。将边 AC 沿 CE 翻折，使点 A 落在 AB 上的点 D 处；在将边 BC 沿 CF 翻折，使点 B 落在 CD 的延长线上的点 B' 处，两条折痕与斜边 AB 分别交于点 E ，F ，则线段 B'F 的长为 4/5 。

图（11）

解析：

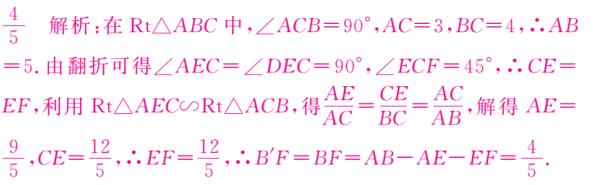
解析图（5）

三、解答题

17、在 13×13 的网格图中，已知 △ABC 和点 M（1,2）。

（1）以点 M 为位似中心，画出 △ABC 的位似图形 △A'B'C' ，使 △ABC 和 △A'B'C' 的位似比为 2 ；

（2）写出 △A'B'C' 的各顶点坐标。

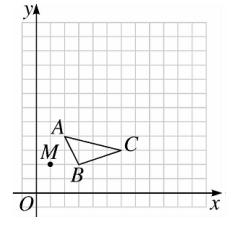
图（12）

解答过程：

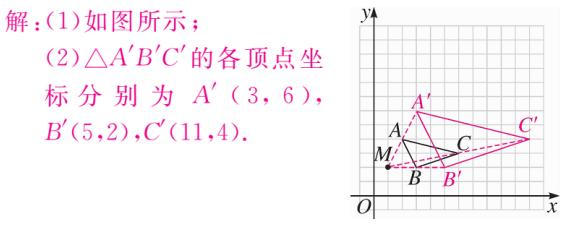
解析图（6）

18、如图，M，N 为山两侧的两个村庄，为了两村交通方便，打一直线涵洞，测量 M，N 两点之间的直线距离。选择测量点 A，B，C 点 B，C 分别在 AM，AN 上，现测得 AM = 1 千米，AN = 1.8 千米， AB = 54 千米，BC = 45 千米 ， AC = 30 千米 。

求：M ,N 两点之间的直线距离。

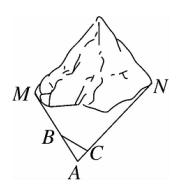
图（13）

解答过程：

解析图（7）

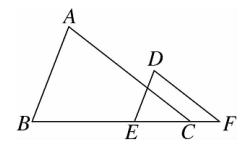
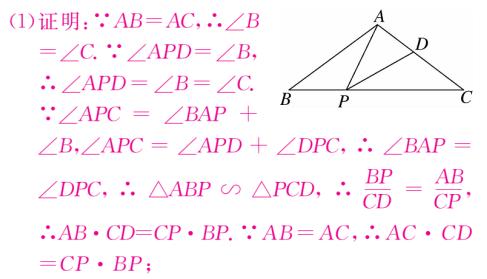
19、如图，在 △ABC 中，AB = AC ，点 P，D 分别是 BC ， AC 边上的点，∠APD = ∠B 。

（1）求证：AC · CD = CP · BP ；

（2）若 AB = 10 ，BC = 12 ，当 PD∥AB 时，求 BP 的长。

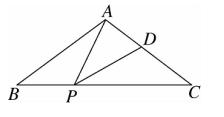
图（14）

解答过程：

解析图（8）

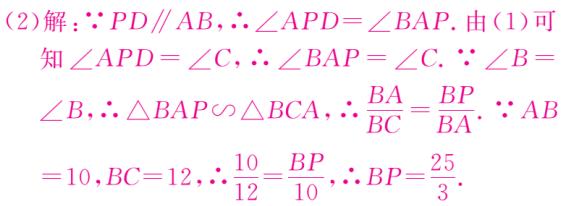
解析图（9）