中考数学，专题复习93：与圆有关的动点综合题型

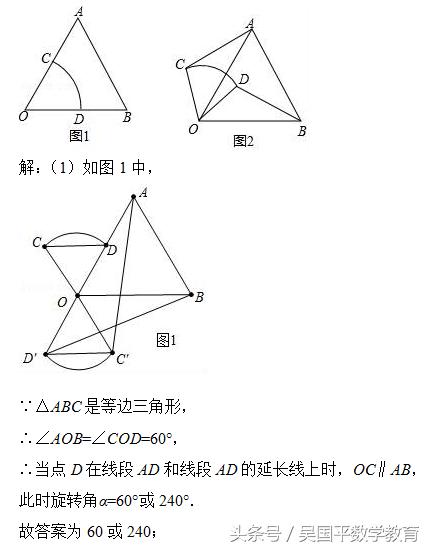
在等边△AOB中，将扇形COD按图1摆放，使扇形的半径OC、OD分别与OA、OB重合，OA=OB=2，OC=OD=1，固定等边△AOB不动，让扇形COD绕点O逆时针旋转，线段AC、BD也随之变化，设旋转角为α．（0＜α≤360°）

（1）当OC∥AB时，旋转角α=　 　度；

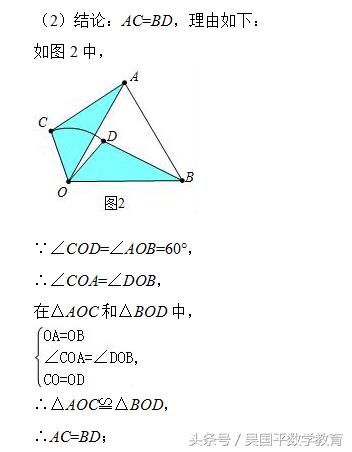
发现：（2）线段AC与BD有何数量关系，请仅就图2给出证明．

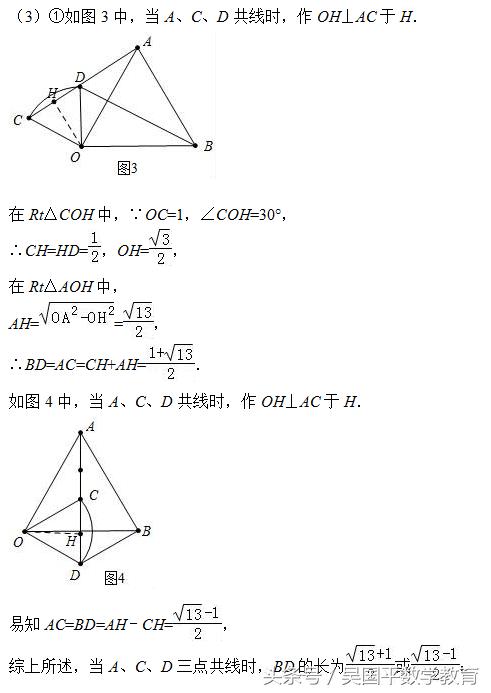
应用：（3）当A、C、D三点共线时，求BD的长．

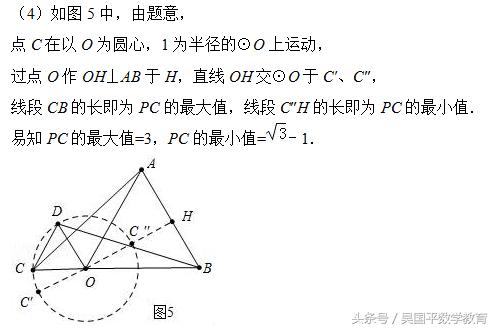
拓展：（4）P是线段AB上任意一点，在扇形COD的旋转过程中，请直接写出线段PC的最大值与最小值．

考点分析：

圆的综合题．

题干分析：

（1）如图1中，易知当点D在线段AD和线段AD的延长线上时，OC∥AB，此时旋转角α=60°或240°．

（2）结论：AC=BD．只要证明△AOC≌△BOD即可．

（3）在图3、图4中，分别求解即可．

（4）如图5中，由题意，点C在以O为圆心，1为半径的⊙O上运动，过点O作OH⊥AB于H，直线OH交⊙O于C′、C″，线段CB的长即为PC的最大值，线段C″H的长即为PC的最小值．易知PC的最大值=3，求得PC的最小值．