初中知识点精华

有理数的分类

⑴正数和零统称为非负数；⑵负数和零统称为非正数；

⑶正整数和零统称为非负整数；⑷负整数和零统称为非正整数.

数轴

数轴：规定了原点、正方向和单位长度的直线.

有理数与数轴的关系： 一切有理数都可以用数轴上的点表示出来. 在数轴上，右边的点所对应的数总比左边的点所对应的数大. 正数都大于 0，负数都小于 0，正数大于一切负数. 注意：数轴上的点不都代表有理数，如π .

相反数

相反数：只有符号不同的两个数互称为相反数．

特别地，0 的相反数是 0.

相反数的性质：

(1) 几何意义：一对相反数在数轴上应分别位于原点两侧，并且到原点的距离相等．

(2) 求任意一个数的相反数，只要在这个数的前面添上“—”号即可． 一般地，数 a 的相反数是-a；这里以 a 表示任意一个数，可以为正数、0、负数，也可以是 任意一个代数式．注意-a不一定是负数．

(3) 重符号的化简：一个正数前面不管有多少个“＋”号，都可以全部去掉； 一个正数前面有偶数个“－”号，也可以把“－”号全部去掉； 一个正数前面有奇数个“－”号，则化简后只保留一个“－”号。

绝对值

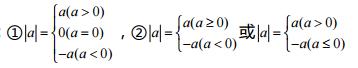
1、绝对值的几何意义：一个数 a 的绝对值就是数轴上表示 a 的点与原点的距离数 a 的绝对值∣a∣

2、绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0 的绝对值是 0.

3、绝对值的性质：

4、绝对值的非负性

非负性：若有几个非负数的和为0 ，那么这几个非负数均为0

2、绝对值的非负性；若 ∣a∣+∣b∣+∣c∣=0，则必有a =0，b =0 ，c =0 有理数的加法

有理数加法法则：

①同号两数相加，取相同的符号，并把绝对值相加.

②绝对值不相等的异号两数相加，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值.

有理数加法的运算技巧：

①分数与小数均有时，应先化为统一形式.

②带分数可分为整数与分数两部分参与运算.

③多个加数相加时，若有互为相反数的两个数，可先结合相加得零. ④若有可以凑整的数，即相加得整数时，可先结合相加.

⑤若有同分母的分数或易通分的分数，应先结合在一起.

⑥符号相同的数可以先结合在一起.

有理数的减法

有理数减法法则：

减去一个数，等于加这个数的相反数. a-b =a +（-b）- = +

有理数减法的运算步骤：

①把减号变为加号（改变运算符号）

②把减数变为它的相反数（改变性质符号）

③把减法转化为加法，按照加法运算的步骤进行运算.

有理数的加减混合运算

有理数加减混合运算的步骤：

①把算式中的减法转化为加法；

②省略加号与括号；

③利用运算律及技巧简便计算，求出结果. - = - - + - ( ) ，

有理数乘法运算律：

①两个数相乘，交换因数的位置，积相等. ab=ba = (乘法交换律)

②三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等：abc= a( bc) (乘法结合律)

③一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加. a (b+c) =ab+ac (乘法分配律) 有理数的除法

有理数除法法则：

除以一个不等于 0 的数，等于乘这个数的倒数. 同号得正，异号得负，并把绝对值相除； 0 除以任何一个不等于 0 的数，都得 0. 有理数除法的运算步骤：首先确定商的符号，然后再求出商的绝对值. 有理数的乘方与科学计数法

有理数的乘方： 求 n 个相同因数的积的运算叫做乘方，乘方的结果叫做幂，在 n a 中，a 叫做底数，n 叫做 指数，读作 a 的 n 次幂。 负数的奇数次幂是负数，负数的偶数次幂是正数； 正数的任何次幂都是正数，0 的任何次幂都是 0

有效数字：从一个数左边第一个非 0 数字起，到末位数字止，所有数字都是这个数的有效数字． 如：0.00027 有两个有效数字：2，7 ；1.2027 有 5 个有效数字：1，2，0，2，7． 近似数：近似数与准确数的接近程度，可以用精确度表示 精确到 0.1Û 精确到十分位；精确到 0.001Û 精确到千分位 有理数的混合运算 有理数的混合运算 1、先乘方，再乘除，最后加减； 2、同级运算，一般从左到右进行,当然也可交换顺序（加减属于同级运算，乘除属于同级运算） 3、如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。