中考数学，专题复习94：与切线有关的几何综合题

典型例题分析1：

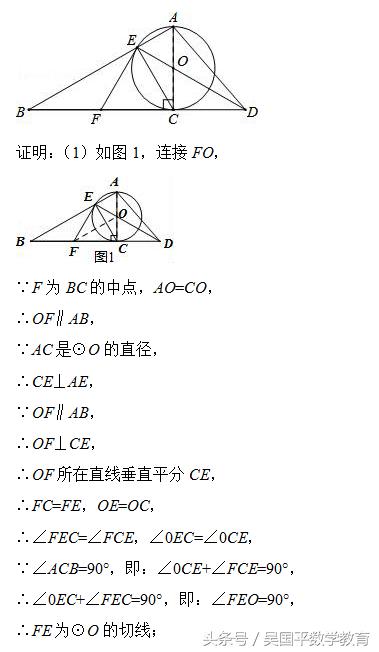
已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．

（1）求证：EF是⊙O的切线；

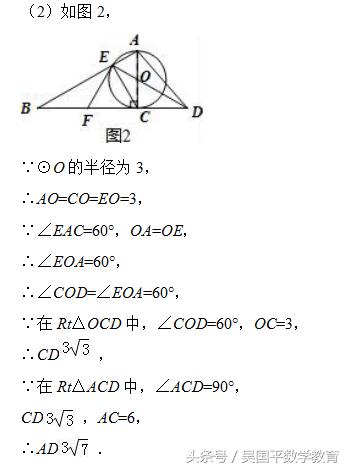
（2）若⊙O的半径为3，∠EAC=60°，求AD的长．

考点分析：

切线的判定．

题干分析：

（1）连接FO，由F为BC的中点，AO=CO，得到OF∥AB，由于AC是⊙O的直径，得出CE⊥AE，根据OF∥AB，得出OF⊥CE，于是得到OF所在直线垂直平分CE，推出FC=FE，OE=OC，再由∠ACB=90°，即可得到结论．

（2）证出△AOE是等边三角形，得到∠EOA=60°，再由直角三角形的性质即可得到结果．

典型例题分析2：

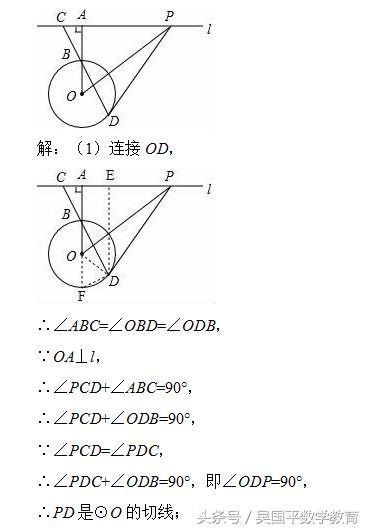
如图，直线l与⊙O相离，过点O作OA⊥l，垂足为A，OA交⊙O于点B，点C在直线l上，连接CB并延长交⊙O于点D，在直线l上另取一点P，使∠PCD=∠PDC．

（1）求证：PD是⊙O的切线；

（2）若AC=1，AB=2，PD=6，求⊙O的半径r和△PCD的面积．

考点分析：

切线的判定．

题干分析：

（1）连接OD，知∠ABC=∠OBD=∠ODB，由∠PCD+∠ABC=90°知∠PCD+∠ODB=90°，结合∠PCD=∠PDC可得∠ODP=90°，即可得证；

（2）由∠PCD=∠PDC知PC=PD=6、PA=5，根据PA2+AO2=PD2+OD2可得r=7/4；延长AO交⊙O于点F，连接DF，证△ABC∽△DBF得AB/DB=BC/BF，即可知DB的值，作DE⊥PC于点E，由△CAB∽△CED知AB/ED=CB/CD，求得DE=24/5，从而求得△PCD的面积．

解题反思：

本题主要考查切线的判定与性质、等边对等角、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质及勾股定理是解题的关键．