一、基础常考点:
二次函数的图像和性质、确定二次函数的表达式、二次函数的应用、二次函数与一元二次方程。
二、考点专练:
1、二次函数的图像和性质:
① 抛物线 y = -( x +2 )^2 - 5 的顶点坐标是 (C)。
A、(-2,5) B、(2,5) C、(-2,-5) D、(2,-5)
② 抛物线 y = x^2 + 2x + 3 的对称轴是 (B)。
A、直线 x = 1 B、直线 x = -1 C、直线 x = -2 D、直线 x = 2
③ 抛物线 y = 3x^2 - 3 向右平移 3 个单位长度,得到新抛物线的表达式为 (A)。
A、y = 3( x - 3 )^2 - 3 B、y = 3x^2 C、y = 3( x + 3 )^2 - 3 D、y = 3x^2 - 6
④ 若点 A(2,y1),B(-3,y2),C(-1,y3)三点在二次函数 y = x^2 - 4x - m 的图像上,则 y1 , y2 , y3 的大小关系是 (C)。
A、y1 > y2 > y3 B、y2 > y1 > y3 C、y2 > y3 > y1 D、y3 > y1 > y2
⑤ 已知二次函数 y = -x^2 + 2x +3 , 当 x ≥ 2 时,y 的取值范围是 (B)。
A、y ≥ 3 B、y ≤ 3 C、y > 3 D、y < 3
⑥ 对于二次函数 y = x^2 - 2mx - 3 ,下列结论错误的是 (C)。
A、它的图像与 x 轴有两个交点
B、方程 x^2 - 2mx = 3 的两根之积为 -3
C、它的图像的对称轴在 y 轴的右侧
D、x< m ,y 随 x 的增大而减小
⑦ 直线 y = ax + b 与抛物线 y = ax^2 + bx + c (a ≠ 0)的大致图像是 (D)。
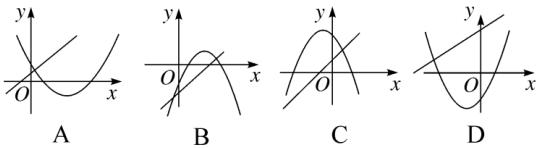
图(1)
⑧ 若二次函数 y = x^2 - 2x + m 的图像与 x 轴有两个交点 ,则 m 的取值范围是 m < 1 。
⑨ 二次函数 y = -2ax^2 + 4ax + 3 的图像与 x 轴有两个交点,其中一个交点的坐标为 (-1,0),则关于 x 的一元二次方程 -2ax^2 + 4ax + 3 = 0 的解为 x1 = -1 , x2 = 3 。
⑩ 已知二次函数 y = -x^2 + 4x 。
(1)用配方法把该二次函数化为 y = a( x - h )^2 + k 的形式,并指出函数图像的对称轴和顶点坐标;
(2)求这个函数图像与 x 轴的交点坐标。
解答过程:

图(2)
⑪ 如图,抛物线 y = x^2 + bx + c 经过坐标原点,并与 x 轴交于点 A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点 B ,且 S△OAB = 3 ,求点 B 的坐标 。
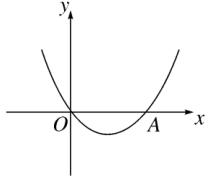
图(3)
解答过程:

图(4)

图(5)
2、求二次函数的表达式:
① 如图,抛物线的函数表达式为 (D)。
A、y = x^2 - x + 2 B、y = x^ + x + 2 C、y = -x^2 - x + 2 D、y = -x^2 + x + 2
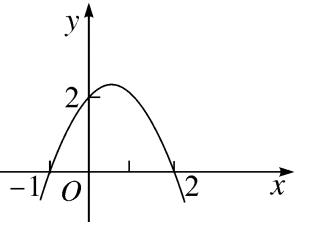
图(6)
② 根据表中的自变量 x 与函数 y 的对应值,可判断此函数解析式为 (D)。
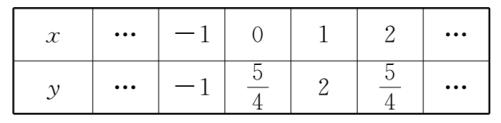
图(7)
A、y = x B、y = -1/x C、y = 3/4 ( x - 1 )^2 + 2 D、y = -3/4 ( x - 1 )^2 + 2
③ 二次函数的图像如图所示,则其表达式为 y = -x^2 + 2x + 3 。
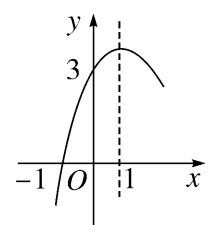
图(8)
④ 已知二次函数 y = x^2 + bx + c 的图像与 y 轴交于点 C(0,-6),与 x 轴的一个交点 坐标是 A(-2,0)。
(1)求二次函数的表达式,并写出顶点 D 的坐标;
(2)将二次函数的图像沿 x 轴向左平移 5/2 个单位长度后,当 y < 0 , 求 x 的取值范围 。
解答过程:

图(9)

图(10)
3、二次函数的应用:
① 如图,桥拱是抛物线形,其函数表达式为 y =( -1/4) x^2 , 当水位线在 AB 位置时,水面宽为 12 m,这时水面离桥顶的高度为 (D)。
A、 3 m B、2√6 m C、4√3 m D、9 m
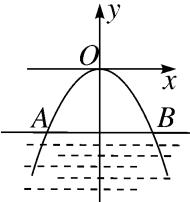
图(11)
② 如图,在边长为 6 cm 的正方形 ABCD 中,点 E、F、G、H 分别从点 A、B、C、D 同时出发,均以 1 cm /s的速度向点 B、C、D、A 匀速运动,当点 E 到达点 B 时,四个点同时停止运动。在运动工程中,当运动时间为 多少 s 时,四边形 EFGH 的面积最小,其最小值是多少 cm^2 ?
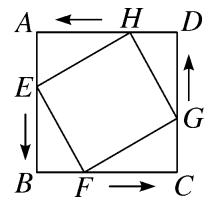
图(12)
答案: 3 , 18 。
③ 某企业研发了一种新产品,已知研发、生产这种产品的成本为 30 元/件 ,且年销售量 y(万件)关于售价 x(元/件)的函数表达式为 :
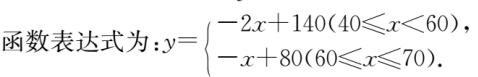
图(13)
(1)若企业销售该产品获得的年利润为 W(万元),请直接写出年利润 W(万元)关于售价 x(元/件)的函数表达式;
(2)当该产品的售价 x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若要使企业销售该产品的年利润不少于 750 万元,试确定该产品的售价 x(元/件)的取值范围 。
解答过程:
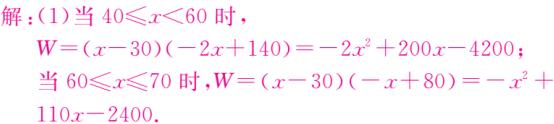
图(14)

图(15)

图(16)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论