平面直角坐标系及函数
【知识梳理】
(一)基本知识点
1.平面直角坐标系的概念
两条互相过原点且垂直的数轴构成平面直角坐标系。
2.平面直角坐标系的特征
原点坐标(0,0);
第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-);
x 轴的点(a,0);y 轴的点(0,a);
第一、三象限角平分线上的点(a,a);
第二、四象限角平分线上的点(-a,a);
3.平面直角坐标系中的点与实数对的关系
坐标系内的点与有序实数对是一一对应的,不同位置点的坐标特征不同;
在坐标系中由一个坐标可以确定一个点的位置,不同位置点的坐标也是不同的;
同一平面内一个点在不同的坐标系中坐标也不相同。

点A(a,b)关于y 轴的对称点的坐标为(-a,b);
点A(a,b)关于原点的对称点的坐标为(-a,-b);
点A(a,b)关于直线y=x的对称点的坐标为(b,a);
点A(a,b)关于直线y=-x的对称点的坐标为(-b,-a);
(3)点的旋转变换
旋转改变的是位置而不是形状,明确旋转前后的对应关系,作垂直,求垂线段的长可得点的坐标。
(4)位似变换后点的坐标
以点A(a,b)所在图形以原点为位似中心,位似比是m时,点A的对应点坐标为(ma ,mb)。
6.函数的定义
在某一变化过程中,有两个变量x和y,给定一个x的值,就有唯一一个确定的y值与它相对应,则y是x的函数,x是自变量。
函数的基本特征:有两个变量x和y ,y随着x的变化而变化,给定一个x的值就有一个y与之相对应。
7.函数的表达形式
3种函数表达形式以及其特点:
(1)解析法:能准确反映整个变化过程中自变量和函数值的对应关系,但实际问题中,有的函数关系不一定能用解析式表示;
(2)列表法:能简单明了地表示自变量和函数值的对应关系,但有局限性;
(3)图象法:能直观地反映出函数的性质和变化规律,画函数图象的一般方法:列表;描点;连线。
8.函数自变量的取值范围
自变量的取值要使实际问题或式子有意义。
确定自变量取值范围的方法:
(1)当函数关系式是一个只含有一个自变量的整式时,自变量是全体实数;
(2)当函数关系式表示实数时,自变量的取值必须使实际问题有意义;
(3)当函数关系式是一个分式时,自变量的取值范围是使分母不为0的实数;
(4)当函数关系式是二次根式时,自变量的取值范围是使被开方数不小于0的实数;
(5)当函数关系式中自变量同时含在分式和二次根式中时,自变量的取值范围是它们的公共取值范围。
9.函数中两个变量的变化规律
在某一变化过程中,变量y随x的变化而变化,x是自变量,y是因变量,y随着x的增大而增大,或y随着x的增大而减小。,
【考点解析】
考点一.平面直角坐标系的特点
【例1】在平面直角坐标系中,点P(m﹣3,4﹣2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】D1:点的坐标.
【分析】分点P的横坐标是正数和负数两种情况讨论求解.
【解答】解:①m﹣3>0,即m>3时,﹣2m<﹣6,
4﹣2m<﹣2,
所以,点P(m﹣3,4﹣2m)在第四象限,不可能在第一象限;
②m﹣3<0,即m<3时,﹣2m>﹣6,
4﹣2m>﹣2,
点P(m﹣3,4﹣2m)可以在第二或三象限,
综上所述,点P不可能在第一象限.
故选A.
考点二:坐标系中的距离
【例2】如图,点A(﹣2,1)到y轴的距离为( )
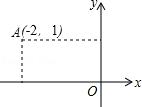
考点: 点的坐标.
分析: 根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
解答: 解:点A的坐标为(﹣2,1),则点A到y轴的距离为2.
故选C.
点评: 本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的长度,到y轴的距离等于
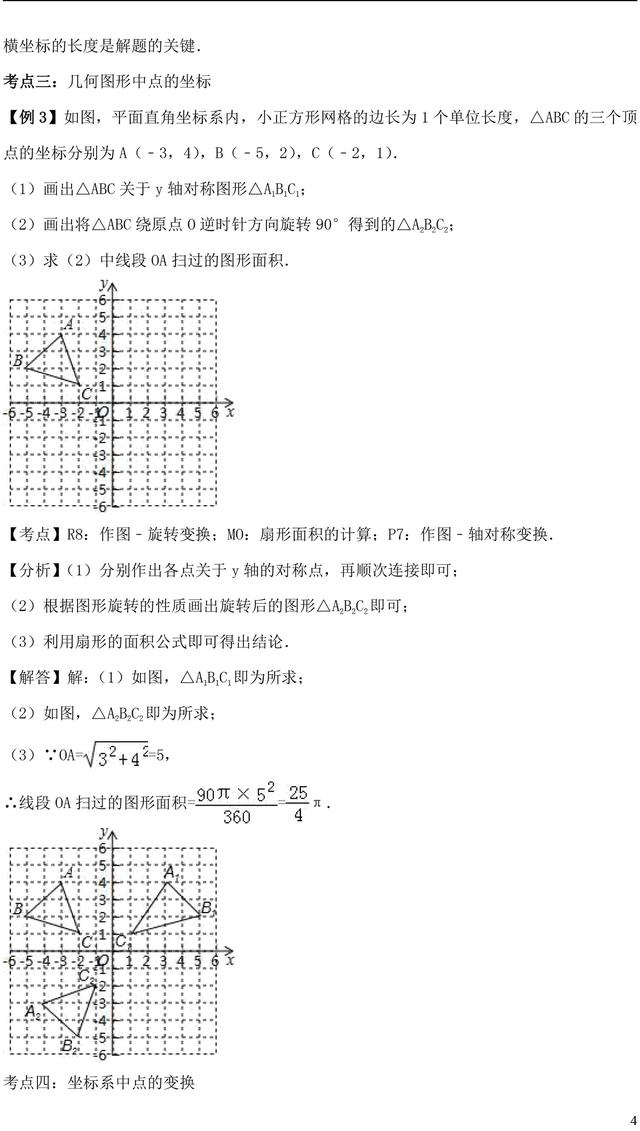


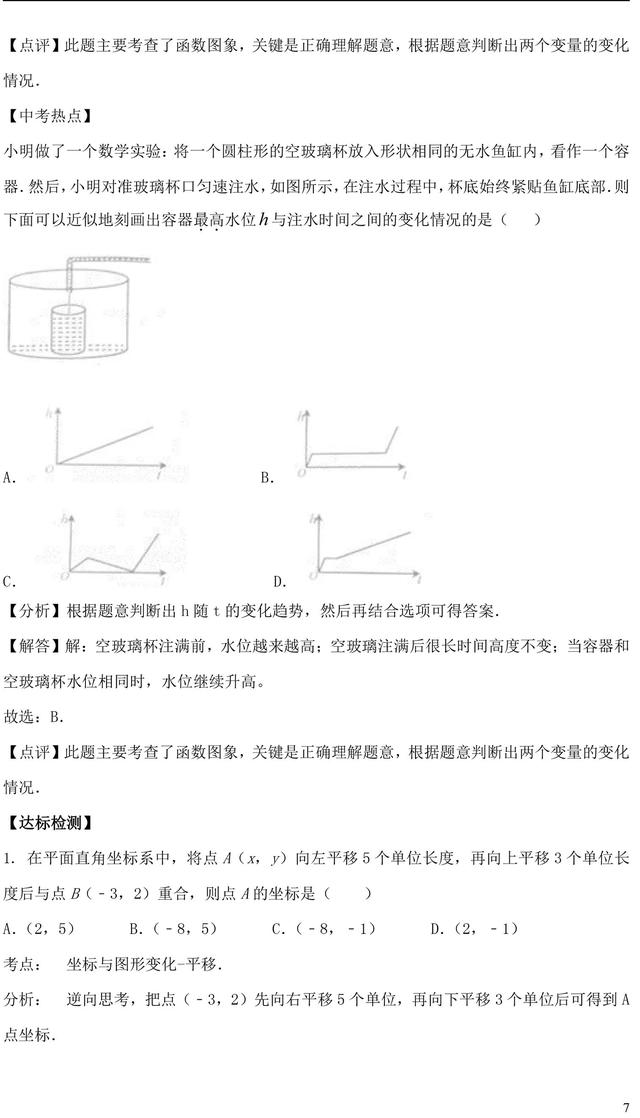




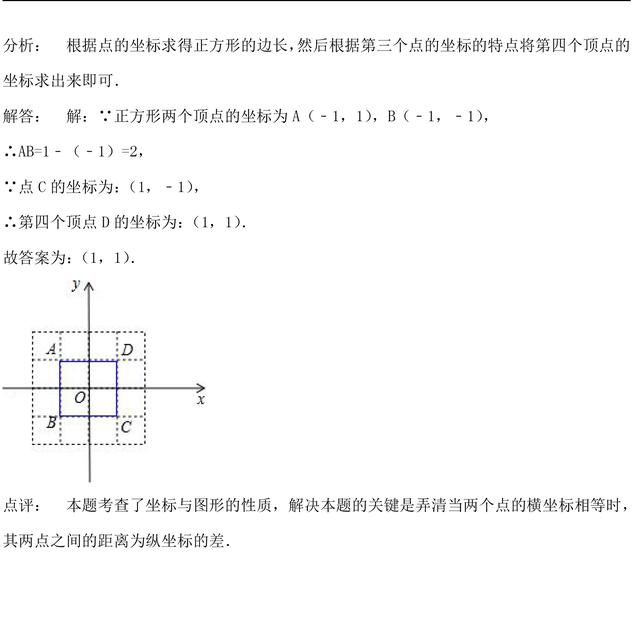
 加载中,请稍侯......
加载中,请稍侯......
精彩评论