高考数学，典型例题分析87：三角函数中的恒等变换应用

在△ABC中，内角A，B，C的对边分别为a，b，c，已知a﹣b=2，c=4，sinA=2sinB．

（Ⅰ）求△ABC的面积；

（Ⅱ）求sin（2A﹣B）．

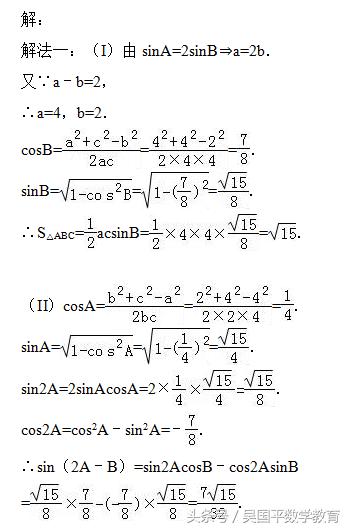
考点分析：

三角函数中的恒等变换应用．

题干分析：

解法一：（I）由已知及正弦定理可求a，b的值，由余弦定理可求cosB，从而可求sinB，即可由三角形面积公式求解．

（II）由余弦定理可得cosA，从而可求sinA，sin2A，cos2A，由两角差的正弦公式即可求sin（2A﹣B）的值．

解法二：（I）由已知及正弦定理可求a，b的值，又c=4，可知△ABC为等腰三角形，作BD⊥AC于D，可求出BD的值，即可求三角形面积．

（II）由余弦定理可得cosB，即可求sinB，由（I）知A=C⇒2A﹣B=π﹣2B．从而sin（2A﹣B）=sin（π﹣2B）=sin2B，代入即可求值．

解题反思：

三角函数是高中数学教材的一个重点内容，也是高考数学常考的要点，高考考查的着力点，三角函数恒等变形方面的技巧能够为解题节省很多时间。

三角恒等变是研究三角函数有关计算及三角函数的图像与性质的基础之一，尤其是在考查三角函数的图像与性质时，往往要用三角恒等变换对解析式进行化简变形。