一、利用同弧或等弧转化圆周角与圆心角:
1、如图、已知 CD 是 ⊙O 的直径,过点 D 的弦 DE 平行于半径 OA ,若 ∠D = 50°,则 ∠C 的度数是 (A)。
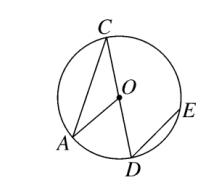
图(1)
A、25° B、30° C、40° D、50°
2、如图、在 ⊙O 中,AB弧等于 AC弧,∠AOB = 40°,则 ∠ADC 的度数是 (C)。
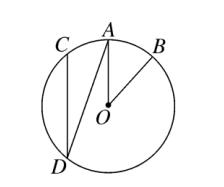
图(2)
A、40° B、30° C、20° D、15°
3、如图、点 A、B、C 在 ⊙O 上,∠A = 36° ,∠C = 28° ,则 ∠B 的度数为 (C)。
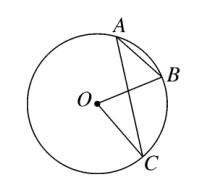
图(3)
A、100° B、72° C、64° D、36°
4、如图、⊙O 的直径 CD 经过弦 EF 的中点 G ,∠DCF = 20° ,则 ∠EOD = 40° 。
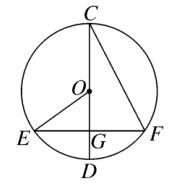
图(4)
二、利用圆内接四边形转化角:
5、四边形 ABCD 内接于 ⊙O ,若 ∠BOD = 138° ,则它的一个外角 ∠DCE 等于 (A)。
A、69° B、42° C、48° D、38°
6、如图、四边形 ABCD 内接于 ⊙O ,∠BCD = 100° ,AC 平分 ∠BAD ,则 ∠BDC 的度数为 40° 。
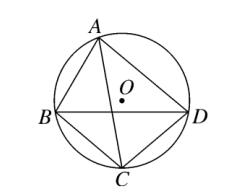
图(5)
7、如图、在 ⊙O 的内接五边形 ABCDE 中,∠CAD = 35°,则 ∠B + ∠E = 215° 。
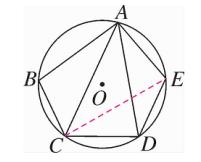
图(6)
解答过程:

图(7)
三、利用直径构造直角三角形转化角:
8、如图、若 AB 为 ⊙O 的直径,CD 是 ⊙O 的弦,∠ABD = 65°,则∠BCD 的度数为(A)。
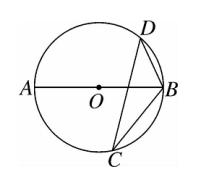
图(8)
A、25° B、45° C、55° D、75°
9、如图、AB 是半圆的直径,点 D 是弧 AC 的中点,∠ABC = 50°,则 ∠DAB 的度数是 65°。
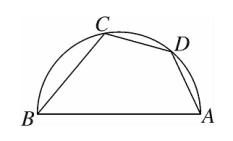
图(9)
解析:

图(10)
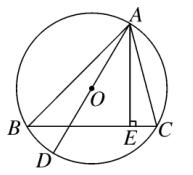
10、如图、△ABC 的顶点均在 ⊙O 上,AD 为 ⊙O 的直径,AE⊥BC 于 E 。
求证: ∠BAD = ∠EAC 。
图(11)
证明:
图(12)
四、利用特殊数量关系构造特殊角转化角:
11、如图、将 ⊙O 沿弦 AB 折叠,圆弧恰好经过圆心 O ,点 P 是优弧 AMB 上一点,则 ∠APB 的度数为 (D)。
A、45° B、30° C、75° D、60°
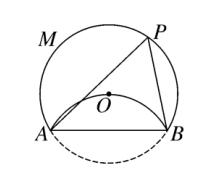
图(13)
解析:

图(14)
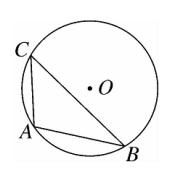
12、如图、△ABC 内接于 ⊙O ,AB = 2 ,⊙O 的半径为 √2 ,则 ∠C = 45° 。
图(15)
解析:
连接 OA 、OB ;
因为 OA = OB = √2 , AB = 2 ;
所以 OA^2 + OB^2 = AB^2 ;
所以 ∠AOB = 90° 。
所以 ∠C = 1/2 ∠AOB = 45° 。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论