一、圆与三角函数的综合:
1、如图, AB 是 ⊙O 的直径,C 是 ⊙O 上的点,过点 C 做 ⊙O 的切线交 AB 的延长线于点 E ,若 ∠A = 30°,
则 sinE 的值为 (A)。
A、1/2 B、√2/2 C、√3/2 D、√3/3
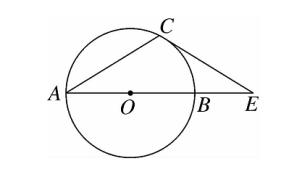
图(1)
2、如图,以点 O 为圆心的两个圆中,大圆的弦 AB 切小圆于点 C ,OA 交小圆于点 D 。若 OD = 2 ,
tan∠OAB = 1/2 , 则 AB 的长是 (C)。
A、4 B、2√3 C、8 D、4√3
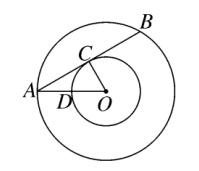
图(2)
3、如图,点 D(0,3),O(0,0),C(4,0) 在 ⊙A 上,BD 是 ⊙A 的一条弦,则 sin∠OBD 的值为 (D)。
A、1/2 B、3/4 C、4/5 D、3/5
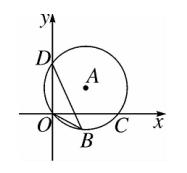
图(3)
4、如图、 AB 为 ⊙O 的直径,以 AB 为直角边作直角△ABC ,∠CAB = 90° ,斜边 BC 与 ⊙O 交于点 D ,过点 D 作 ⊙O 的切线 DE 交 AC 于点 E ,DG⊥AB 于点 F ,交 ⊙O 于点 G 。
①求证:E 是 AC 的中点;
②若 AE = 3 ,cos∠ACB = 2/3,求弦 DG 的长 。
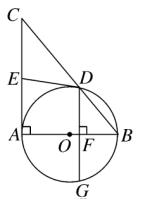
图(4)
解答过程:
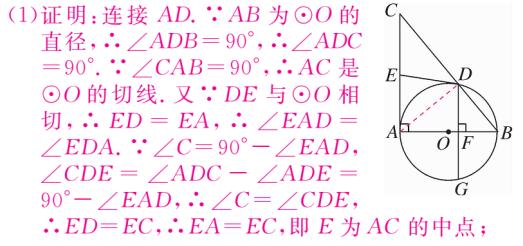
图(5)

图(6)
二、圆与相似的综合:
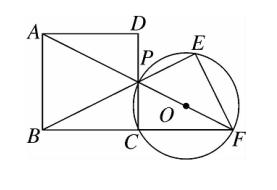
5、如图,边长为 2 的正方形 ABCD 中, P 是 CD 的中点,连接 AP 并延长,交 BC 的延长线于点 F ,作△CPF 的外接圆 ⊙O ,连接 BP 并延长交 ⊙O 于点 E ,连接 EF ,则 EF 的长为 (D)。
A、3/2 B、5/3 C、3√5/5 D、4√5/5
图(7)
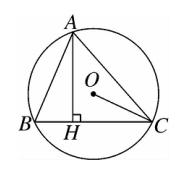
6、如图,△ABC 内接于 ⊙O ,AH⊥BC 于点 H ,若 AC = 24 ,AH = 18 ,⊙O 的半径 OC = 13 ,
则 AB = 39/2 。
图(8)

图(9)
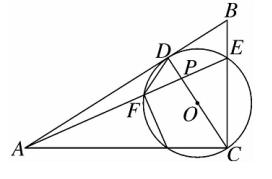
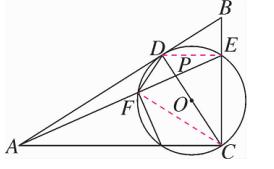
7、如图、△ABC 中,∠ACB = 90° ,D 为 AB 上一点,以 CD 为直径的 ⊙O 交 BC 于点 E ,连接 AE 交 CD 于点 P ,交 ⊙O 于点 F ,连接 DF ,∠CAE = ∠ADF 。
①判断 AB 与 ⊙O 的位置关系,并说明理由;
②若 PF : PC = 1:2 , AF = 5 , 求 PC 的长 。
图(10)
解:
(1)AB 是 ⊙O 的切线 。
理由:
图(11)
连接 DE , CF
∵ CD 是 ⊙O 的直径 ,∴ ∠DEC = ∠DFC = 90° 。
∵ ∠ACB = 90° ,∴ ∠DEC + ∠ACE = 180° 。
∴ DE∥AC ,∴ ∠CAE = ∠DEA = ∠DCF 。
∵ ∠DFC = 90° ,∴ ∠DCF + ∠CDF = 90° 。
∵ ∠ADF = ∠CAE = ∠DCF ,∴ ∠ADF + ∠CDF = 90° 。
∴ ∠ADC = 90° , ∴ CD⊥AD ,AB 是 ⊙O 的切线 。
(2)

图(12)
三、圆与四边形的综合:
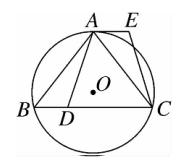
8、如图,⊙O 是 △ABC 的外接圆,AB弧 = AC弧 ,点 D 在边 BC 上,AE∥BC ,AE = BD 。
(1)求证:AD = CE ;
(2)如果点 G 在线段 DC 上(不与点 D 重合),AG = AD ,求证:四边形 AGCE 是平行四边形。
图(13)
证明:
(1)
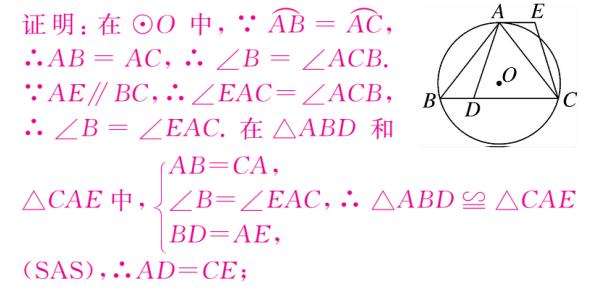
图(14)
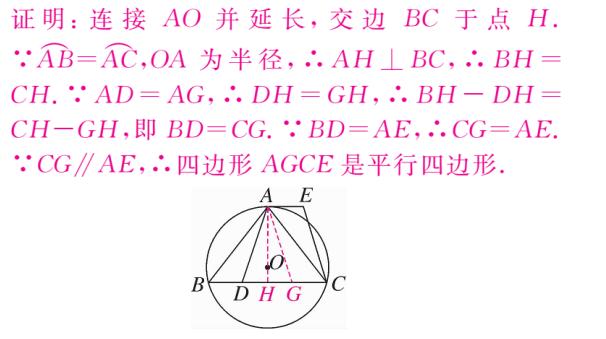
(2)
图(15)
四、坐标系中的圆(代数与几何综合):
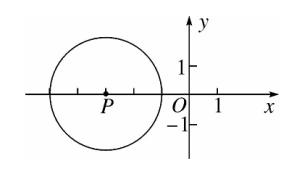
9、如图,在平面直角坐标系 xOy 中,半径为 2 的 ⊙P 的圆心 P 的坐标为 (-3,0),将 ⊙P 沿 x 轴正方向平移,使 ⊙P 与 y 轴相切,则平移的距离为 (B)。
A、1 B、1 或 5 C、3 D、5
图(16)
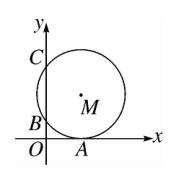
10、如图,在平面直角坐标系中,⊙M 与 x 轴相切于点 A(8,0),与 y 轴分别交于 B(0,4)和点 C(0,16),则圆心 M 到坐标原点 O 的距离是 (D)。
A、10 B、8√2 C、4√13 D、2√41
图(17)
解析:

图(18)
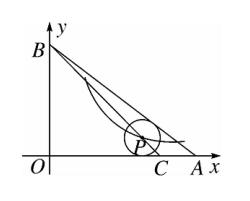
11、如图,在 Rt△OAB 中,OA = 4 ,AB = 5 ,点 C 在 OA 上,AC = 1 。⊙P 的圆心 P 在线段 BC 上,⊙P 与边 AB,AO 都相切。若反比例函数 y = k/x (k ≠ 0)的图像经过圆心 P ,则 K = 5/4 。
图(19)
解析:

图(20)
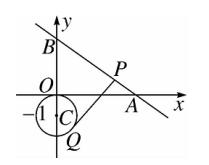
12、如图,直线 y = -3/4 x + 3 与 x 轴,y 轴 分别交于点 A ,B ,点 Q 是以 C(0,-1)为圆心,1 为半径的圆上一动点,过 Q 点的切线交线段 AB 于点 P ,则线段 PQ 的最小值是多少?
图(21)
解析过程:
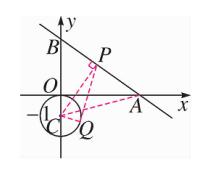
图(21)

图(22)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论