一、常见的几何最值问题:
1、如图、已知直线 l 及点 A、B,在直线 l 上做点 P ,使 PA + PB 最小。
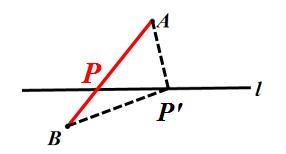
图(1)
当 P 、 A 、 B 三点共线时,PA + PB 最小,最小值为 AB 。
依据:两点之间的线段距离最短。
2、如图、已知直线 l 及点 A、B,在直线 l 上做点 P ,使 PA + PB 最小。
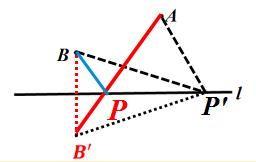
图(2)
当 P 、 A 、 B' 三点共线时,PA + PB 最小,最小值为 AB' 。
依据:两点之间的线段距离最短。
3、如图、已知直线 l 及点 A ,在直线 l 上作点 P ,使 PA 最小。
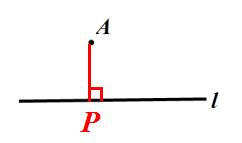
图(3)
依据:垂线段最短。
4、如图、已知直线 l 及点 A、B ,点 B 在直线 l 上,在直线 l 上做点 P ,使 PA + 1/2PB 最小。
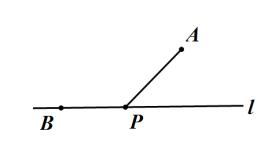
图(4)
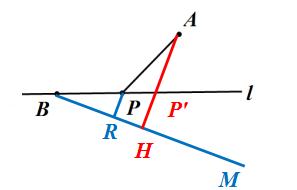
图(5)
作法:
①过终点 B 在直线 l 下方作一条射线 BM ,使之与 BP 构成的角满足 sina = 1/2 , a = 30° ;
②过起点 A 做该射线的垂线 AH ;
③该垂线与直线 l 的交点 P' 即为所求。
依据:当 A、P'、H 三点共线时,P‘A + 1/2P'B 最小,最小值为 AH 。
二、典型例题:
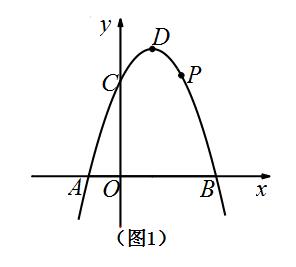
例题、如图1所示,在平面直角坐标系中,抛物线 y = -x^2 + 2x +3 与 x 轴交于 A、B 两点,与 y 轴交于点 C ,点 D 是抛物线的顶点,点 P(3/2 , 15/4)是抛物线上一点。
(1)点 A、B、C、D 的坐标分别是多少?
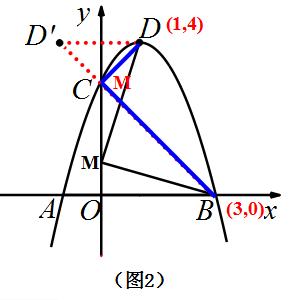
(2)如图2,M 为 y 轴上一动点,求 BM + DM 最小值及此时点 M 的坐标。
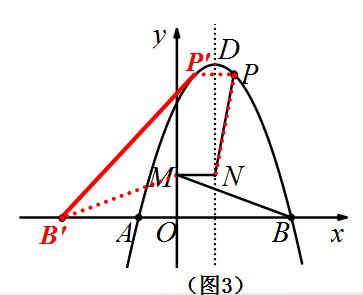
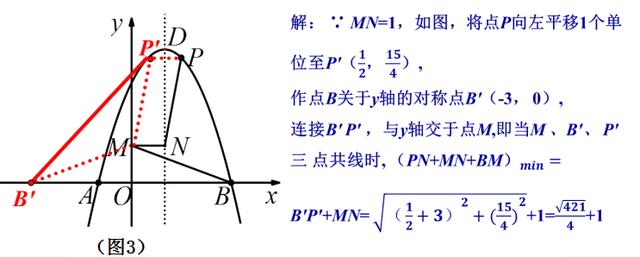
(3)如图3,M 为 y 轴上一动点,N 为抛物线对称轴上一动点,且 MN⊥y轴,求 PN+MN+BM 的最小值。
图(6)
图(7)
图(8)
解:
(1)A(-1,0); B(3,0); C(0,3);D(1,4)。
(2)

图(9)
(3)
图(10)
三、总结:
1、2个原理: ①两点之间,线段最短;②垂线段最短。
2、2种手段: ①轴对称;②平移。
3、1种思想:转化的思想。
 加载中,请稍侯......
加载中,请稍侯......
精彩评论