常见的出题套路是这样的：

例题：某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为x元（x为正整数），每个月的销售利润为y元．

（1）当每件商品的售价是多少元时，每个月的利润刚好是2250元？

（2）当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

【分析】（1）如果每件商品的售价每上涨1元，则每个月少卖2件，可得销售量为100﹣2（x﹣60），销售量乘以利润即可得到等式：

[100﹣2（x﹣60）]（x﹣40）=2250，解答即可；

（2）将（1）中的2250换成y即可解答。

【解析】（1）[100﹣2（x﹣60）]（x﹣40）=2250，解得：x1=65，x2=85．

（2）由题意：

y=[100﹣2（x﹣60）]（x﹣40）=﹣2x2+300x﹣8800；

y=﹣2（x﹣75）2+2450，

当x=75时，y有最大值为2450元．

答：当售价定为75时，每个月可获得最大利润，最大的月利润是2450元．

教师点评：本题考查了一元二次方程的应用和二次函数的应用。解题关键：建立二次函数表达式，根据二次函数性质特点求得最大值——最大的月利润。

还可以有更灵活的出题套路：

例题1

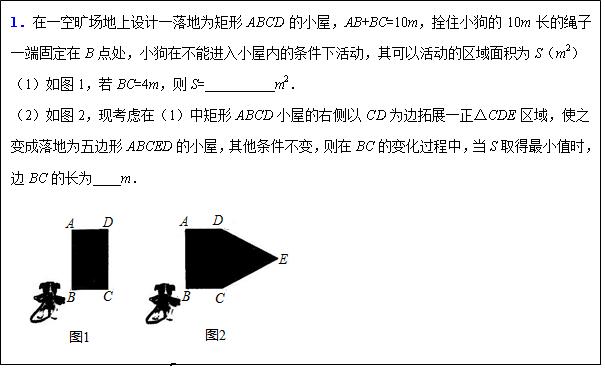
本题从解决实际问题出发，利用了二次函数最值来解决问题，体现了数学的实用性。

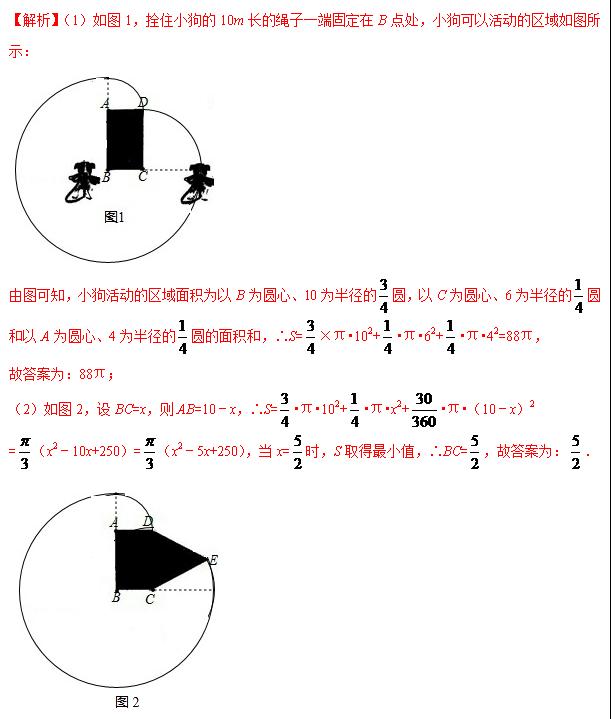
例题1解析

教师点评：本题考查了二次函数的应用；等边三角形的判定与性质；矩形的性质；最值问题；二次函数的最值；属于综合性问题。解题关键：根据绳子的长度结合图形得出其活动区域及利用扇形的面积公式表示出活动区域面积。

二次函数还可以和平面几何相结合：

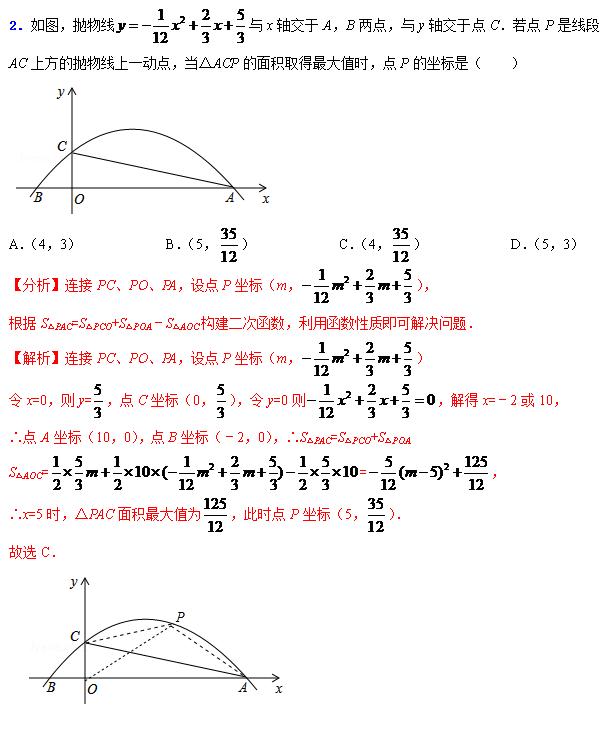
例题2

教师点评：抛物线与x轴的交点；二次函数的最值；最值问题；动点型综合题型。解题关键：根据三角形面积构建二次函数关系式，利用二次函数性质解决问题。

还可以综合性更强、题目更复杂：

【分析】（1）找出直线y=mx+1与y轴的交点坐标，将其代入抛物线解析式中即可求出n的值；再根据抛物线的解析式找出顶点坐标，将其代入直线解析式中即可得出结论；

（2）找出直线与反比例函数图象的交点坐标，由此设出抛物线的解析式，再由直线的解析式找出直线与x轴的交点坐标，将其代入抛物线解析式中即可得出结论；

（3）由抛物线解析式找出抛物线与y轴的交点坐标，再根据抛物线的解析式找出其顶点坐标，由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式，找出该直线与x、y轴的交点坐标，结合三角形的面积找出面积S关于k的关系上，由二次函数的性质即可得出结论。

例题3（1）解析

例题3（2）解析

例题3（3）解析

教师点评：本题综合了二次函数和一次函数性质，是一道综合性非常强的函数问题。解题关键：准确表示出抛物线顶点坐标，然后根据函数表达式，代入三角形面积公式求解。

总结：二次函数向来是中考命题的热门题型，是因为二次函数可以和数学很多知识结合，容易命出复杂题型，所以二次函数的题目也有一定的难度。而二次函数最值的解题思路：充分利用二次函数表达式与图像的特点，就可以解决。