高考数学，典型例题分析83：立体几何相关的综合题型

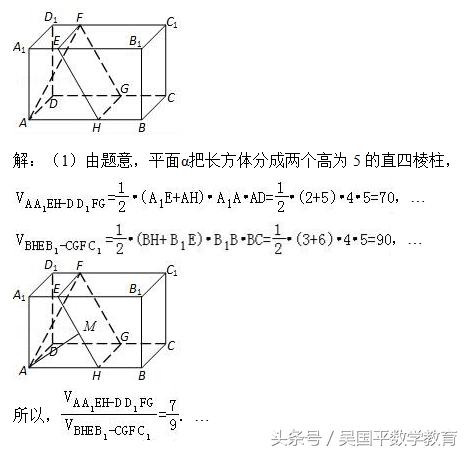
如图，在长方体ABCD﹣A1B1C1D1中，AB=8，BC=5，AA1=4，平面α截长方体得到一个矩形EFGH，且A1E=D1F=2，AH=DG=5．

（1）求截面EFGH把该长方体分成的两部分体积之比；

（2）求直线AF与平面α所成角的正弦值．

考点分析：

直线与平面所成的角；棱柱、棱锥、棱台的体积．

题干分析：

（1）由题意，平面α把长方体分成两个高为5的直四棱柱，转化求解体积推出结果即可．

（2）解法一：作AM⊥EH，垂足为M，证明HG⊥AM，推出AM⊥平面EFGH．通过计算求出AM=4．AF，设直线AF与平面α所成角为θ，求解即可．

解法二：以DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，求出平面α一个法向量，利用直线AF与平面α所成角为θ，通过空间向量的数量积求解即可．

解题反思：

立体几何试题在高考中占了很大的分量，研究其解题方法显得尤为重要，直线与平面所成角问题是高考立体几何试题中几乎每年都会考到的问题,每年都有很多考生在这方面丢分。

线线角、线面角、二面角是高考考查的重点知识，三类角号称"三角"，而线面角又是重中之重，求线面角的方法源于定义,而又超越于定义。