中考数学，专题复习80：四边形相关综合题型

如图，▱ABCD中，AD=2AB，点E在BC边上，且CE=AD/4，

F为BD的中点，连接EF．

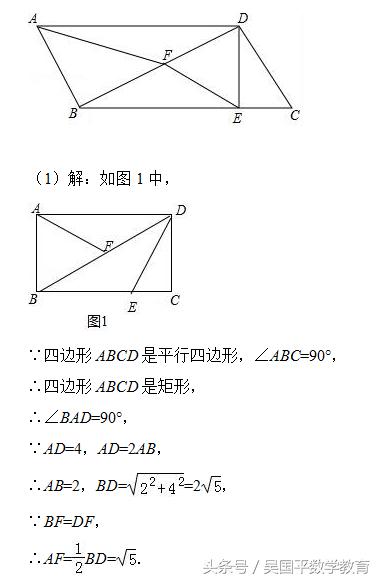
（1）当∠ABC=90°，AD=4时，连接AF，求AF的长；

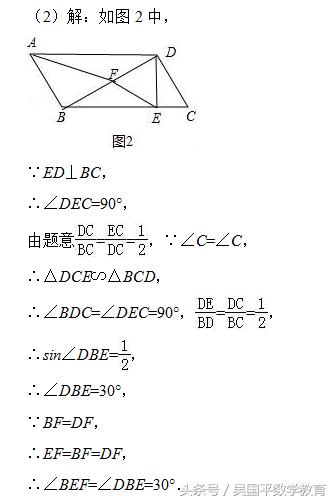
（2）连接DE，若DE⊥BC，求∠BEF的度数；

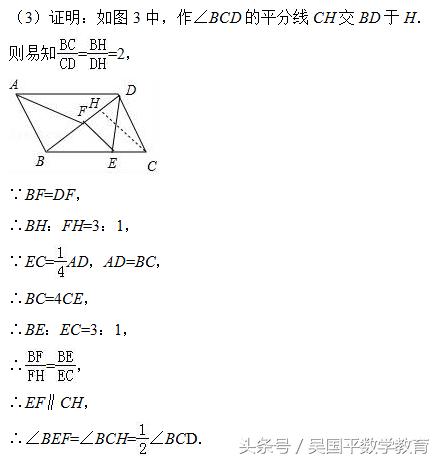
（3）求证：∠BEF=∠BCD/2．

题干分析：

（1）如图1中，首先证明四边形ABCD是矩形，利用勾股定理求出BD，再利用直角三角形斜边的中线的性质即可解决问题；

（2）如图2中，由题意DC/BC=EC/CD=1/2，由∠C=∠C，推出△DCE∽△BCD，推出∠BDC=∠DEC=90°，DE/BD=DC/BC=1/2，推出sin∠DBE=1/2，可得∠DBE=30°，由此即可解决问题；

（3）如图3中，作∠BCD的平分线CH交BD于H．则易知BC/CD=BH/DH=2，想办法证明EF∥CH即可；

解题反思：

本题考查平行四边形的性质、直角三角形斜边中线的性质、锐角三角函数、平行线的判定．角平分线的性质定理等知识，解题的关键灵活运用所学知识解决问题，属于中考压轴题．