高考数学，典型例题分析80：频率分布表

植树节期间我市组织义工参加植树活动，为方便安排任务将所有义工按年龄分组：第l组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的部分频率分布表如下：

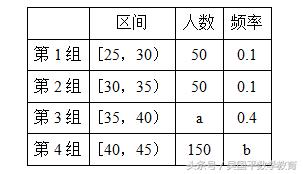
（1）求a，b的值；

（2）现在要从年龄较小的第l，2，3组中用分层抽样的方法随机抽取6人担任联系人，在第l，2，3组抽取的义工的人数分别是多少？

（3）在（2）的条件下，从这6人中随机抽取2人担任本次活动的宣传员，求至少有1人年龄在第3组的概率．

解：（1）根据题意知，50÷0.1=500，

所以共有500人参加活动；

a=500×0.4=200，b=150/500=0.3；

（2）因为第1，2，3组共有50+50+200=300人，

利用分层抽样在300名员工中抽取6人，每组抽取的人数分别为：

第1组的人数为6×50/300=1，

第2组的人数为6×50/300=1，

第3组的人数为6×200/300=4，

∴第1，2，3组分别抽取1人，1人，4人；

（3）由（2）可设第1组的1人为A，第2组的1人为B，

第3组的4人分别为C1，C2，C3，C4，

则从6人中抽取2人的所有可能结果为：

（A，B），（A，C1），（A，C2），（A，C3），（A，C4），

（B，C1），（B，C2），（B，C3），（B，C4），

（C1，C2），（C1，C3），（C1，C4），

（C2，C3），（C2，C4），（C3，C4），共有15种．

其中2人年龄都不在第3组的有：（A，B），共1种；

所以至少有1人年龄在第3组的概率为P=1﹣1/15=14/15．

考点分析：

频率分布表．

题干分析：

（1）根据频率=频数/样本容量求出参加活动的总人数，再求a、b的值；

（2）计算分层抽样的抽取比例，用抽取比例乘以每组的频数，可得每组抽取人数；

（3）利用列举法写出从6人中随机抽取2人的所有基本事件，再用对立事件的概率公式计算对应的概率即可．