中考数学相似与几何图形的综合问题

一、三角形与相似的综合问题：

例题1、一块直角三角板 ABC 按如图放置，顶点 A 的坐标为 （0,1），直角顶点 C 的坐标为 （-3,0），

∠B = 30° ，则点 B 的坐标为多少？

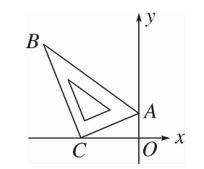
图（1）

解析：

图（2）

例题2、如图、Rt△ABC 中 ，∠ACB = 90°，AC = 3 ，BC = 4 ，将边 AC 沿 CE 翻折 ，使点 A 落在 AB 上的点 D 处。在将边 BC 沿 CF 翻折， 使点 B 落在 CD 的延长线上的点 B‘ 处，两条折痕与斜边 AB 分别交于点 E,F ，则线段 B‘F 的长是多少？

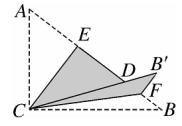
图（3）

解析：

图（4）

二、四边形与相似的综合问题：

例题3、现有多个全等直角三角形，先取三个拼成如图 ① 所示的形状 ，R 为 DE 的中点 ，BR 分别交 AC、CD 于 P 、 Q ，易证 BP : PQ : QR = 3 ： 1 ： 2 。

（1）若取 4 个全等直角三角形拼成如图 ② 所示的形状，S 为 EF 的中点，BS 交 AC、CD、DE 于 P、Q、R ，则 BP：PQ ： QR ：RS 的比是多少？

（2）若取 5 个全等直角三角形拼成如图 ③ 所示的形状，T 为 FG 的中点，BT 交 AC、CD、DE、EF 于 P、Q、R ，S 则 BP：PQ ： QR ：RS ：ST 的比是多少？

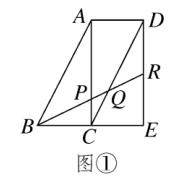
图（5）

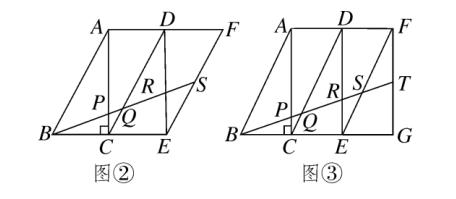
图（6）

解析：

图（7）

图（8）

总结：根据已知条件，充分利用图形中平行的条件，连续用相似三角形的判定与性质，得出线段之间的比例关系。“遇平行，想相似；用相似，得比例”是解决相似形问题的常用思路之一。

例题4、如图、矩形 ABCD 中，AB = 8 ， BC = 4 ，点 E 在 AB 上 ，点 F 在 CD 上 ，点 G、H 在对角线 AC 上。若四边形 EGFH 是棱形，则 AE 的长是多少？

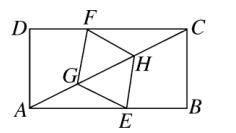
图（9）

解析：

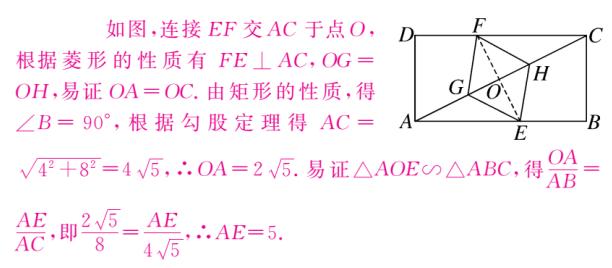
图（10）

三、运用相似解决几何图形中的动点问题：

例题5、如图、在平面直角坐标系中，以点 B（0，8）为端点的射线 BG∥x 轴，点 A 是射线 BG 上的一个动点（点 A 与点 B 不重合），在射线 AG 上取 AD = OB ，做线段 AD 的垂直平分线，垂足为 E ，与 x 轴交于点 F ，过点 A 作 AC⊥OA ，交射线 EF 于点 C ，连接 OC ,CD ，设点 A 的横坐标为 t 。

（1）用含 t 的式子表示点 E 的坐标为 （t + 4 , 8）;

（2）当 t 为何值时，∠OCD = 180° 。

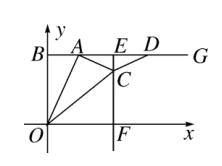
图（11）

解析：

图（12）