一、反比例函数与相似三角形:
例题1、如图一次函数 y = kx + b (k < 0)的图像经过点 C(3,0),且与两坐标轴围成的三角形的面积为 3 。
(1)求该一次函数的表达式;
(2)若反比例函数 y = m/x 的图像与该一次函数的图像交于二、四象限内的 A、B 两点,且 AC = 2BC ,求 m 的值。
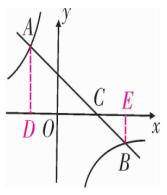
图(1)
解:

图(2)

图(2)
二、反比例函数与三角形的形状:
例题2、如图、在同一直角坐标系中,一次函数 y = √3 x - 2 的图像和反比例函数 y = k/x 的图像的一个交点为 A(√3 , m)。
(1)求 m 的值及反比例函数的表达式;
(2)若点 P 在 x 轴上,且 △AOP 为等腰三角形,请直接写出点 P 的坐标。
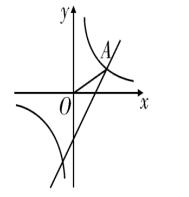
图(3)
解:

图(4)

图(5)
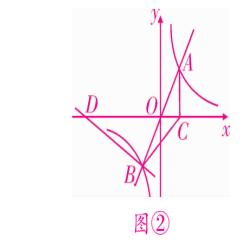
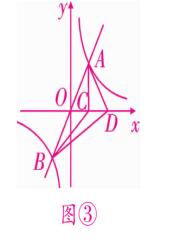
例题3、如图、正比例函数 y = 2x 的图像与反比例函数 y = k/x 的图像交于 A、B 两点,过点 A 做 AC⊥x 轴于点 C ,连接 BC ,若 △ABC 的面积为 2 。
(1)求 k 的值 ;
(2)x 轴上是否存在一点 D ,使 △ABD 为直角三角形?若存在,求出点 D 的坐标,若不存在,请说明理由。
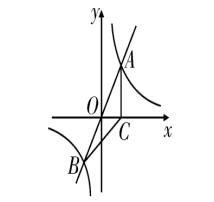
图(6)
解:
(1) k = 2 ;
(2)
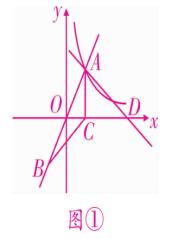
图(7)

图(8)
图(9)

图(10)
图(11)

图(12)
三、反比例函数与四边形:
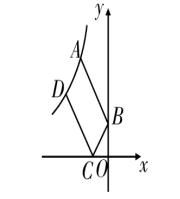
例题4、如图、点 A(1-√5 ,1 + √5)在双曲线 y = k/x (x < 0 , k ≠ 0 )上。
(1)求 k 的值;
(2)在 y 轴上取点 B(0,1),双曲线上是否存在一点 D ,使得以 AB,AD 为邻边的平行四边形 ABCD 的顶点 C 在 X 轴的负半轴上?若存在,求出点 D 的坐标,若不存在,请说明理由。
图(13)
解:
图(14)

图(15)

图(16)
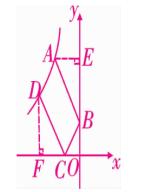
例题5、如图、在平面直角坐标系中,棱形 ABCD 的顶点 C 与原点 O 重合,点 B 在 y 轴的正半轴上,点 A 在反比例函数 y = k/x (k > 0 , x > 0)的图像上,点 D 的坐标为 (4,3)。
(1)求 K 的值 ;
(2)若将棱形 ABCD 沿 x 轴正方向平移,当棱形的顶点 D 落在函数 y = k/x (k > 0 , x > 0)的图像上,求棱形 ABCD 沿 x 轴正方向平移的距离。
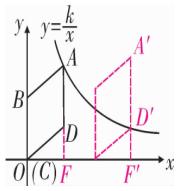
图(17)
解:

图(18)

图(19)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论