基本图形分析法：角平分线和平行线的组合图形（五）

【分析方法导引】当几何问题中出现角平分线和平行线的组合关系式，就可以想到要应用等腰三角形的基本图形进行证明。然后就应用将角的边的平行线与角平分线及角的另一边相交或将角平分线的平行线与角的一边及另一边的反向延长线相交的方法找到等腰三角形的基本图形。再应用角平分线、平行线、等腰三角形中任何两个性质成立就可以推得第三个性质成立的方法来完成分析。

例15 如图3-50，已知：△ABC中，AE是∠A的外角平分线，F是BC的中点，过F作EA的平行线交AB于G。求证：BG=1/2（AB-AC）。图3-50

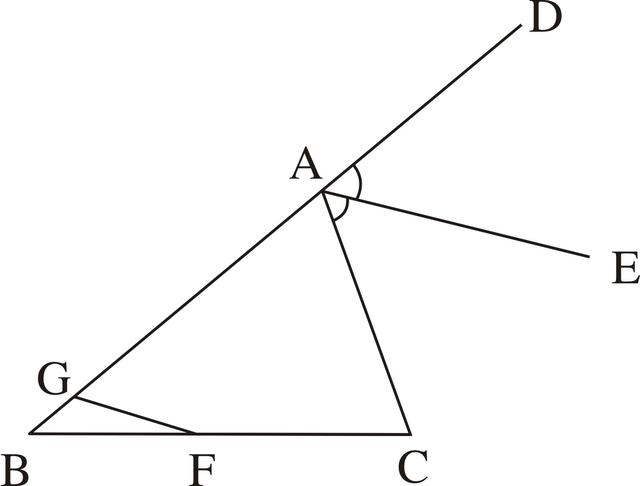
图3-50

分析：本题条件中出现AE是∠A的外角平分线，FG∥EA是角平分线的平行线，所以就一定出现一个等腰三角形的基本图形。由于FG是角平分线的平行线，所以它应和角的一边以及另一边的反向延长线相交组成等腰三角形，而现在GF尚未与角的一边AC相交，所以应先将它们延长到相交，也就是延长GF交AC的延长线于H，即可得△AGH应是一个等腰三角形（如图3-51），也就是由∠DAE=∠CAE和GH∥AE，∠DAE=∠AGH，∠CAE=∠H，得∠AGH=∠H，AG=AH。

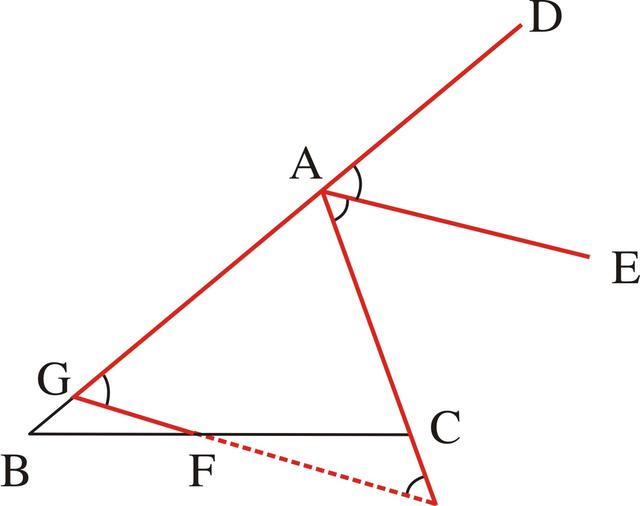
图3-51

由于问题是要证明BG=1/2（AB-AC），所以就有AB-AC=（AG+BG）-（AH-CH）=BG+CH，这样问题就转化为要证BG=CH。

由条件BF=CF，且BC、GH在F点相交，这就出现了BF和CF这两条相等直线是位于一组对顶角（∠BFG和∠CFH）的两边上，而且成一直线，所以可添加一对中心对称型的全等三角形进行证明，添加的方法是过两端点作平行线，并要与过中点的直线相交，于是过C作CK∥AB交GH于K（如图3-52），则由∠BFG=∠CFK，BF=CF，∠B=∠FCK可得△BFG≌△CFK，BG=CK，这样问题又成为要证CK=CH。由于CK∥AB，而且△AGH已经证明是等腰三角形，所以CH=CK就可以证明。

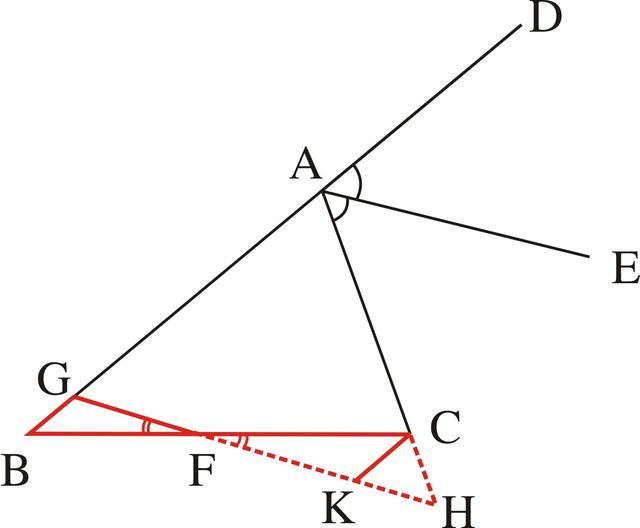
图3-52

在上述分析中，由于已经出现的角平分线AE的平行线GF尚未与角的一边AC相交，所以要得到等腰三角形也可以再作一条同时与AB、AC相交的AE的平行线，于是过C作EA的平行线交AB于H（如图3-53），那就即可证明AH=AC，这样AB-AC就等于AB-AH=BH，也就是要证明G是BH的中点。由于已知F是BC的中点，出现了两个中点，是多个中点问题，所以可应用三角形中位线的基本图形性质进行证明（如图3-54），也就是要证明BG=HG可转化成要证GF∥HC，而由条件GF∥AE，再由作法HC∥AE，所以GF∥HC得以证明。

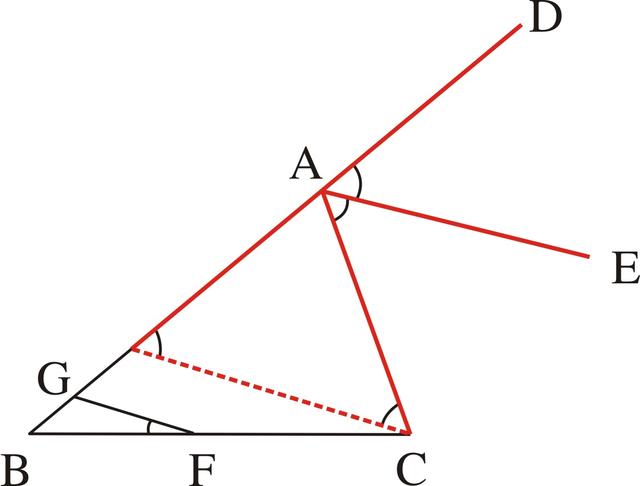
图3-53

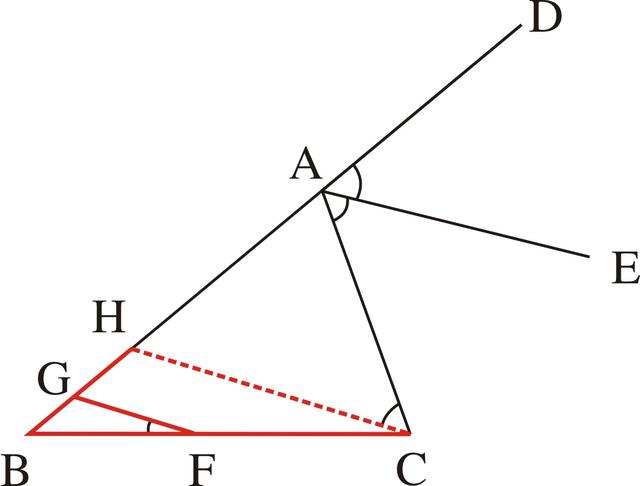
图3-54

例16 如图3-55，已知：E是正方形ABCD的边CD的中点，F是CE的中点。求证：∠BAF=2∠DAE。

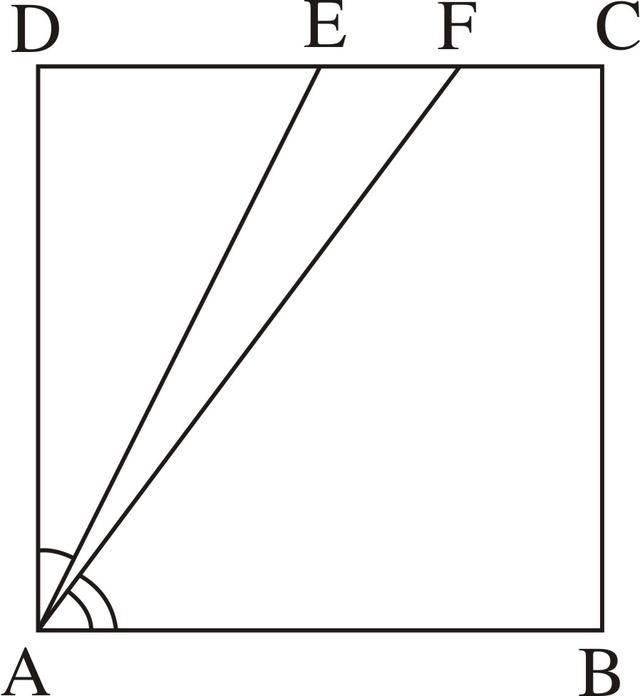
图3-55

分析：本题要证明的结论∠BAF=2∠DAE是两个角之间的倍半关系，所以可根据角的倍半关系的定义，将这个倍角（∠BAF）二等分，也就是作这个角的角平分线后，证明这个角的一半与另一个角相等，于是作∠BAF的角平分线AG交BC于G（如图3-56），问题就成为应证∠BAG=∠DAE。

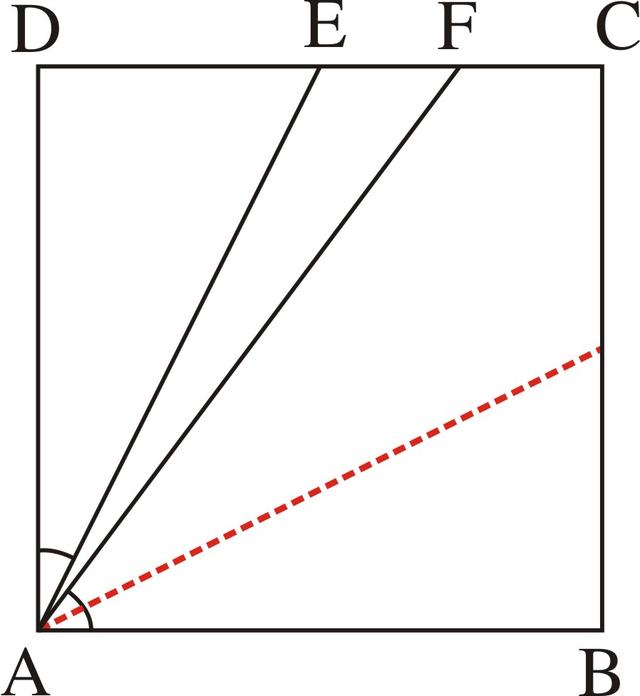
图3-56

在作出了AG是∠BAF的角平分以后，由于条件中给出了四边形ABCD是正方形，DC∥AB，所以就出现了角平分线和平行线的组合关系，这样就必定产生一个等腰三角形的基本图形。由于现在出现的DC是角的一边AB的平行线，所以它应该与角的另一边AF以及角平分线AG相交组成等腰三角形，而目前图形中DC尚未与角平分线AG相交，所以应将它们延长到相交，也就是延长DC交AG的延长线于H（如图3-57），于是由∠BAG=∠FAH和DC∥AB，∠BAG=∠H，可得∠FAH=∠H,FA=FH。

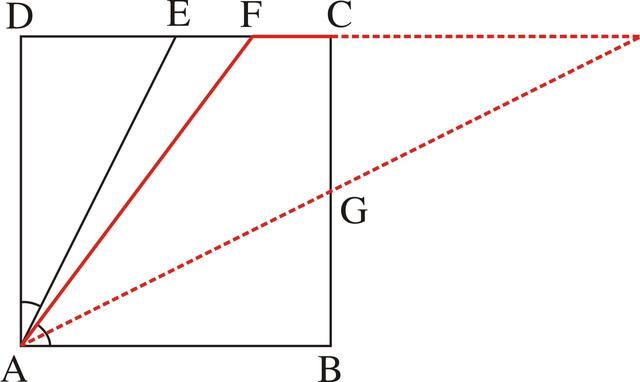
图3-57

由于我们现在要证明的性质是∠BAG=∠DAE，而这两个角可以分别看作是△BAG和△DAE的一个内角，而在这两个三角形中，已经出现了∠B=∠D=90°和AB=AD（即正方形的边长），所以△BAG和△DAE必定是一对全等三角形（如图3-58）。而在证明这一对三角形全等时，由于∠BAG=∠DAE是要证明的结论不能用，那么它的等价性质∠AGB=∠AED也不能用，所以只能考虑再证一组对应边相等的条件。由于条件中给出E是DC的中点，DE=1/2DC，所以考虑与条件有联系的性质，就应证明BG=DE，从而进一步就是要证明G是BC的中点，CG=BG。

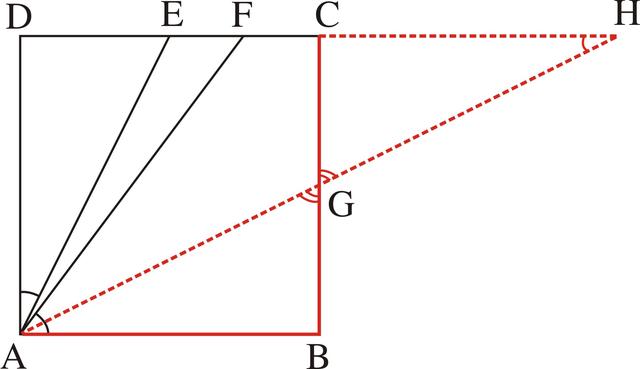
图3-58

由于AH、BC相交于G，所以要证明相等的这两条线段BG和CG就位于一组顶角（∠AGB和∠HGC）的两边而且成一直线，从而就可以应用中心对称型的全等三角形进行证明。根据过两端点B、C的平行线与过中点的直线相交构成全等三角形的方法，就可以找到这对全等三角形应是△AGB和△HGC，在这一对三角形中，对应角相等的性质都已成立，所以就须证明一组对应边相等。由于AB是正方形的边，所以可以考虑证明AB=HC。根据条件FC=1/4CD=1/4AB，可知只须证FH=5/4AB，再由已证明的性质FA=FH，可知要证明的结论又转化为FA=5/4AB。而由DF=3/4AB，AD=AB和∠D=90°，应用勾股定理就可以证明FA=5/4AB，从而完成分析。