一、选择题:
1、抛物线 y = -2x^2 + 3 的顶点在 (y 轴上)。
2、二次函数 y = ax^2 + bx -1 (a ≠ 0)的图像经过点 (1,1),则 a + b + 1 的值是 (3)。
3、抛物线 y = ( x +2 )^2 - 1 可以由抛物线 y = x^2 (先向左平移两个单位,在向下平移一个单位)得到。
4、一条开口向下的抛物线的顶点坐标是 (2,3),则这条抛物线有 (最大值 3)。
5、如图、已知二次函数 y = -x^2 + 2x , 当 -1 < x < a 时,y 随 x 的增大而增大,则实数 a 的取值范围是
(-1 < a ≤ 1)。
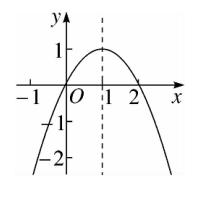
图(1)
6、坐标平面上,某二次函数图像的顶点为 (2,-1),此函数图像与 x 轴相交于 P、Q 两点,且 PQ = 6 。若此函数图像通过 (1,a),(3,b),(-1,c),(-3,d)四点,则 a,b,c,d 之值何者为正 (D)。
A、a B、b C、c D、d
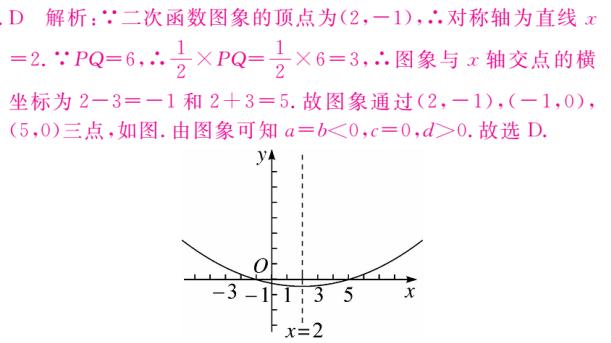
图(2)
7、抛物线 y = ax^2 + bx + c ( a ≠ 0 ) 的图像如图所示,则一次函数 y = ax + b 与反比例函数 y = c/x 在同一平面直角坐标系内的图像大致为 (B)。
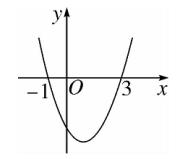
图(3)
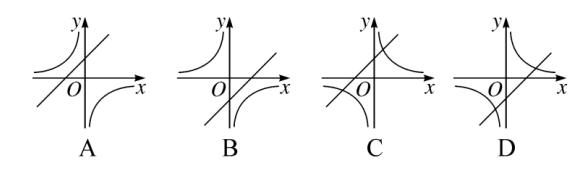
图(4)
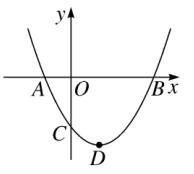
8、如图、二次函数 y = ax^2 + bx + c (a > 0)图像的顶点为 D ,其图像与 x 轴的交点 A,B 的横坐标分别为 -1 和 3 ,则下列结论正确的是 (D)。
图(5)
A、2a - b = 0 B、a + b + c > 0 C、3a - c = 0 D、当 a = 1/2 时,△ABD 是等腰直角三角形
解析:

图(6)
二、填空题:
9、抛物线 y = 2(x - 1 )^2 - 1 与 y 轴的交点坐标是 (0,1)。
10、如果抛物线 y = (2 + k )x^2 - k 的开口向下,那么 k 的取值范围是 (k <-2)。
11、将抛物线 y = -x^2 先向下平移 2 个单位,再向右平移 3 个单位后所得抛物线的解析式为
(y = -x^2 + 6x -11)。
12、若点 A(-5,y1),B(-7/2,y2),C(3/2,y3)为二次函数 y = x^2 + 4x +5 的图像上的三点,则 y1,y2,y3 的大小关系是 (y2<y1<y3)。
13、已知抛物线 y = x^2 + bx + c 的对称轴为直线 x = 2 , 点 A ,B 均在抛物线上,且 AB 与 x 轴平行,其中点 A 的坐标为 (0,3),则点 B 的坐标为 (4,3)。
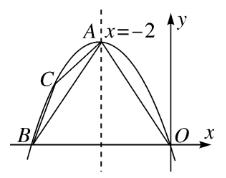
14、如图、在平面直角坐标系中,点 A 在第二象限,以 A 为顶点的抛物线经过原点,与 X 轴负半轴交于点 B ,对称轴为直线 x = 2 ,点 C 在抛物线上,且位于点 A、B 之间(C 不与 A、B 重合)。若△ABC 的周长为 a ,则四边形 AOBC 的周长为 (a + 4)。(用含 a 的式子表示)
图(7)

图(8)
三、简答题:
15、已知二次函数 y = -x^2 + 4x 。
(1)用配方法把该二次函数化为 y = a(x - h )^2 + k 的形式,并指出函数图像的对称轴和顶点坐标;
(2)求这个函数图像与 x 轴的交点的坐标。

图(9)
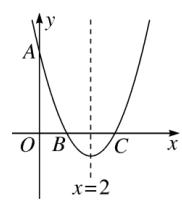
16、如图、已知二次函数 y = x^2 + mx + n 的图像经过 A(0,3),对称轴是直线 x = 2 。
(1)求该函数解析式;
(2)在抛物线上找一点 p ,使 △PBC 的面积是 △ABC 的面积的 2/3 ,求出点 P 的坐标 。
图(10)

图(11)
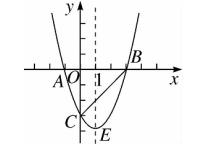
17、如图、抛物线 y = ax^2 + bx -3 (a ≠ 0 ) 的顶点为 E ,该抛物线与 x 轴交于 A、B 两点,与 y 轴交于点 C ,且 BO = OC = 3AO 。
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点 P ,使 △PBC 是等腰三角形?若存在,请写出符合条件的点 P 的坐标;若不存在,请说明理由。
图(12)

图(13)

 加载中,请稍侯......
加载中,请稍侯......
精彩评论