一、同一直角坐标系中判断函数图像:
例题1、当 a ≠ 0 时,函数 y = ax + 1 与函数 y = a/x 在同一坐标系中的图像可能是 (A)。
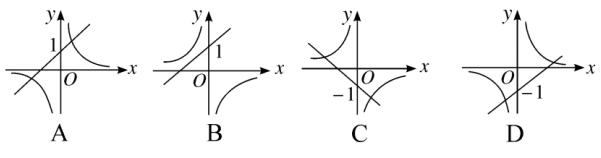
图(1)
二、利用反比例函数的中心对称性求点的坐标或代数式的值:
例题2、已知一个正比例函数的图像与一个反比例函数的图像的一个交点坐标为 (1,3),则另一个交点坐标是 (-1,-3)。
例题3、直线 y = kx (k >0)与双曲线 y = 2/x 交于 A 、B 两点。若 A 、B 两点的坐标分别为 A(x1,y1), B(x2,y2),则 x1y2 + x2y1 的值为多少?
解:由双曲线 y = 2/x 及 y = kx 的中心对称性知 x1 = -x2 , y1 = -y2 ;
所以: x1y2 + x2y1 = -x2y2 - x2y2 = -2x2y2 = -2 × 2 = -4 。
三、利用反比例函数图像与一次函数图像的交点求解:
例题4、如图、在平面直角坐标系中,反比例函数 y1 = 2/x 的图像与一次函数 y = kx + b 的图像交于 A , B 两点,若 y1 < y2 , 则 x 的取值范围是多少?
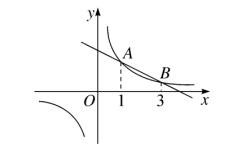
图(2)
解:x < 0 或 1 < x < 3 。
例题5、若反比例函数 y = k/x (k ≠ 0)与一次函数 y = x + 2 的图像没有交点,则 K 的取值范围是多少?
解:令 k/x = x + 2 , 即 x^2 + 2x - k = 0 。
若两图像没有交点,则 △ = 2×2 + 4k < 0 ,所以 k < -1 。
例题6、如图、将函数 y = -x 的图像以点 O 为中心旋转 90° 与函数 y = 1/x 的图像交于点 A ,在将 y = -x 的图像向右平移至点 A ,与 x 轴交于点 B ,则点 B 的坐标为多少?
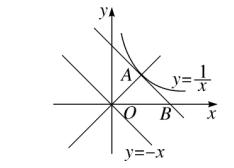
图(3)
解:

图(4)
例题7、如图、已知一次函数 y1 = k1x + b (k1 ≠ 0)的图像与 x 轴, y 轴分别交于 A , B 两点,与反比例函数
y2 = k2/x(k2 ≠ 0) 的图像分别交于 C,D 两点,点 D 的坐标为 (2,-3)点 B 是线段 AD 的中点 。
(1)求一次函数 y1 = k1x + b 与 反比例函数 y2 = k2/x 的解析式;
(2)求 △COD 的面积;
(3)直接写出 y1 >y2 时自变量 x 的取值范围 。
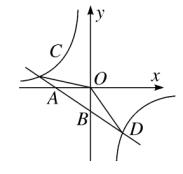
图(5)
解:

图(6)
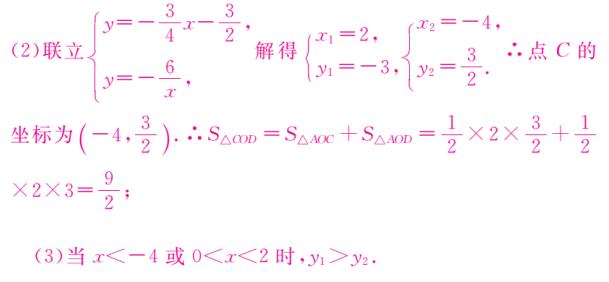
图(7)
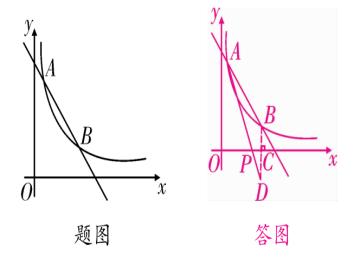
例题8、如图 一次函数 y = -x + 4 的图像与反比例函数 y = k/x (k 为常数,且 k 不等于 0)的图像交于
A(1,a), B 两点。
(1)求反比例函数的表达式及点 B 的坐标;
(2)在 x 轴上找一点 P ,使 PA + PB 的值最小,求满足条件的点 P 的坐标及 △PAB 的面积。
图(8)
解:

图(9)

图(10)

图(11)

图(12)
 加载中,请稍侯......
加载中,请稍侯......
精彩评论